HDU 4832 Chess 排列组合 DP

Chess

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 351    Accepted Submission(s): 124

Problem Description

小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘 上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。





　　图1 黄色部分为棋子所控制的范围

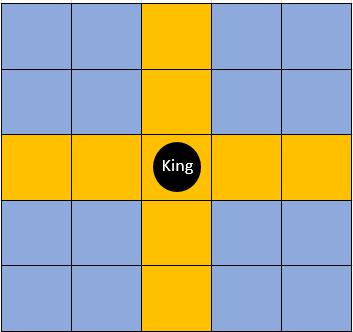
　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x₀,y₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。

　　小良被难倒了。你能写程序解决这个问题吗？

 

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。

每组测试数据只包括一行，为五个整数N,M,K,x₀,y₀。(1≤N,M,K≤1000,1≤x₀≤N,1≤y₀≤M)

 

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

 

Sample Input

2 2 2 1 1 1 2 2 2 1 1

 

Sample Output

Case #1: 2 Case #2: 4

 

Source

2014年百度之星程序设计大赛 - 初赛（第二轮）

题目分析：

最朴素的思想是每个点不断向旁边扩散，每个点第k次的方案数为sum（所有能到这个点的第（k-1）次所在的点的方案数之和），最终答案就是第k次所有点的方案数之和，复杂度大约是O(k*n*m)，系数8，所以超时是定定的。

那么暴力不行我们应该怎么办？可以将横着走和竖着走拆开来考虑，因为这是互不影响的。设起点为（x0， y0），row[k][i]为第k步从起点走到纵坐标为 i 的方案数，col[k][i]为第k步从起点走到横坐标为 i 的方案数那么从起点（x0，y0）到（x，y）走k步的方案数即sum(col[k - d][x] * row[d][y])（d <— 0~k）。将所有横着走d步的方案累加得到cnt[0][d]，所有竖着走d步的方案累加得到cnt[1][d]，由排列组合可知，从横着走选d步，从竖着走选k - d步的组合数为C（k，d）。那么答案就是sum（C（k，d））（d <— 0~k）。算法的时间复杂度大约为O(n * m)，十分优秀了~。

由于状态只于前一次有关，所以用了滚动数组优化，代码如下：

#include 
#include <string.h>
#define MS0(X) memset(X, 0, sizeof(X))
#define REP(i, a, b) for(int i = a; i <= b; ++i)
typedef long long ll;
const int O = 1005;
const int mod = 9999991;
int col[2][O], row[2][O], cnt[2][O], C[O][O], cur;
int n, m, k, x, y, t, cas;
void work(){scanf("%d%d%d%d%d", &n, &m, &k, &x, &y);MS0(col); MS0(row); MS0(cnt);cur = 0;col[0][y] = row[0][x] = cnt[0][0] = cnt[1][0] = 1;REP(i, 1, k){cur ^= 1;MS0(col[cur]); MS0(row[cur]);REP(j, 1, m){if(j - 2 >= 1) col[cur][j] += col[cur ^ 1][j - 2];if(j - 1 >= 1) col[cur][j] += col[cur ^ 1][j - 1];if(j + 1 <= m) col[cur][j] += col[cur ^ 1][j + 1];if(j + 2 <= m) col[cur][j] += col[cur ^ 1][j + 2];col[cur][j] %= mod;cnt[0][i] = (cnt[0][i] + col[cur][j]) % mod;}REP(j, 1, n){if(j - 2 >= 1) row[cur][j] += row[cur ^ 1][j - 2];if(j - 1 >= 1) row[cur][j] += row[cur ^ 1][j - 1];if(j + 1 <= n) row[cur][j] += row[cur ^ 1][j + 1];if(j + 2 <= n) row[cur][j] += row[cur ^ 1][j + 2];row[cur][j] %= mod;cnt[1][i] = (cnt[1][i] + row[cur][j]) % mod;}}ll ans = 0;REP(i, 0, k){ans = (ans + (((ll) cnt[0][i] * cnt[1][k - i]) % mod) * C[k][i]) % mod;}printf("%I64d
", ans);
}
int main(){REP(i, 0, O - 1) C[i][0] = 1;REP(i, 1, O - 1) REP(j, 1, i) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;for(scanf("%d", &t), cas = 1; cas <= t; ++cas){printf("Case #%d:
", cas);work();}return 0;
}