首页 > LTE PUCCH F2 TX/RX汇总

LTE PUCCH F2 TX/RX汇总

TX

TX端的公式如下(下图来自sharetechnote)：

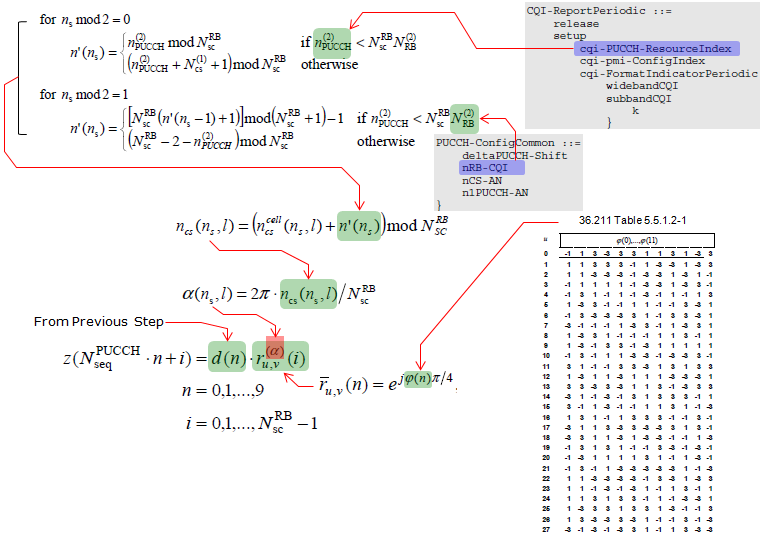
发送端在36.212/36.211中有详细的描述，就是一系列的数学运算，过程概括如下：

编码、加扰、调制的过程暂不介绍，主要介绍下上图中乘以r_uv的过程，公式如下：

$z() = d(n).r^{alpha}_{u,v}(i)$

$d(n)$ : 是调制后的复数，n=0,1...9

下面介绍 $r^{alpha}_{u,v}(i)$ ，参考36.211-5.5.1中r_uv的定义：

$r^{alpha,delta }_{u,v}(n)=e^{jalpha(n+deltafrac{varpi mod2}{2})}overline{r}_{u,v}(n)$ $0leq n< M^{RS}_{sc}$

F2中 $delta$ =0, 所以上式简化为：

$r^{alpha}_{u,v}(n)=e^{jalpha n}overline{r}_{u,v}(n)$

右边有2部分组成： $e^{jalpha n}$ 和 $overline{r}_{u,v}(n)$

1). $e^{jalpha n}$ ：变化在于 $alpha$

F2的 $alpha$ ，参考36.211 - 5.4.2

$alpha_{widetilde{p}}(n_{s},l) = 2pi.n^{(widetilde{p})}_{cs}(n_s.l)/N^{RB}_{sc}$ , $N^{RB}_{sc}=12$

假设： $X=n^{(widetilde{p})}_{cs}(n_s.l)$

简化： $alpha= (2pi/12)X$ , 即： $e^{jalpha n} = e^{j(2pi/12) Xn}$ , 相当于将圆分了N等份。

2). $overline{r}_{u,v}(n)$ : 基序列(base sequence), 可以参考5.5.1.x, 这里我们假如 $M^{RS}_{sc}=N^{RB}_{sc}$ , 则基序列参考5.5.1.2,

$overline{r}_{u,v}(n) = e^{jvarphi (n)pi/4}$ , $0leq nleq M^{RS}_{sc}-1$

可见基序列的变化在于 $varphi (n)$ , 参考36.211中的Table 5.5.1.2-1

$varphi (n)$ 取决于u值，u:sequence-group number, 参考36.211 - 5.5.1.3

这里我们去u值为0，则 $varphi (n)$ 的12个值分别为：

n	0	1	2	3	4	5	6	7	8	9	10	11
$varphi (n)$	-1	1	3	-3	3	3	1	1	3	1	-3	3
$overline{r}_{u,v}(n)$	$e^{j-pi/4}$	$e^{jpi/4}$	$e^{j3pi/4}$	$e^{j-3pi/4}$

可以看到相当于将圆分了4等份。

RE mapping:

RX

信道估计(CE)，计算H:

DMRS 12个RE(1symbol *12sc), 每个RE除以r_uv, 然后12个RE求和得到H。

均衡：

Data12个RE(1symbol *12sc), 每个RE除以r_uv, 然后再除以H,得到一个complex, 2个slot 有10 symbol 传输data, 所以可以得到10个complex, 由于采用QPSK调制(实部和虚部各代表一个bit)，10个complex 转化为20个bit, 20个bit 输入译码器可以得到原始的传输数据。

另外，复数相除，乘以复共轭，

$frac{a}{b} = frac{a.overline{b}}{b.overline{b}} = frac{a.overline{b}}{left | b ight | ^{2}}$

RX端先除以r_uv, 注意 $r^{alpha}_{u,v}(n)=e^{jalpha n}overline{r}_{u,v}(n) =e^{jalpha n} e^{jvarphi (n)pi/4} = e^{j(alpha n+varphi (n)pi/4)}$ , 所以r_uv的模方=1.

接着除以了H, H的的模方不等于1，所以分子共轭乘后，别忘了除以分母的模方.

LTE PUCCH F2 TX/RX汇总

TX

RX

更多相关：

node！！！