运动学

在研究控制机械臂之前，有必要学习一些运动学知识，比如学习反向运动学内容，解决命令任意串行操纵器沿预先计划的轨迹朝向目标的问题等等。

下面是一个大纲，介绍了“运动学-机械手介绍及分类”这个主题下的一些主要的内容。

• 自由度（DoF）
• 参考框架
• 广义坐标
• 联合类型
• 主要类型的串行机械手
• 串行机械手应用

1. 自由度

“自由度”（DoF）是指定义空间机制的位置或配置所需的最小变量数。

实例：两个自由度的机械手

这是一个两个自由度的机械手，其原点时p0(0, 0),中间节点p1， 和最终控制点p2。

下面使用matplotlib来完成对两自由度机械臂的模拟。

import matplotlib.pyplot as plt
import numpy as np# 定义一个函数来计算机械手的位置
def compute_arm_config(link1_length, link2_length, joint0_angle, joint1_angle):joint1_x = link1_length * np.cos(joint0_angle)joint1_y = link1_length * np.sin(joint0_angle)p2_x = joint1_x + link2_length * np.cos(joint1_angle)p2_y = joint1_y + link2_length * np.sin(joint1_angle)return joint1_x, joint1_y, p2_x, p2_y# 随机生成一个机械手的位置
link1_length = np.random.random() * 30 + 20
link2_length = np.random.random() * 30 + 20
joint0_angle = np.random.random() * 2 * np.pi
joint1_angle = np.random.random() * 2 * np.pijoint1_x, joint1_y, p2_x, p2_y = compute_arm_config(link1_length, link2_length, joint0_angle, joint1_angle)print("joint0_angle =", round(joint0_angle * 180 / np.pi, 1), "degrees")
print("joint1_angle =", round(joint1_angle * 180 / np.pi, 1),"degrees")
print("End Effector at x =", round(p2_x, 1),"y =", round(p2_y, 1))base_x = 0
base_y = 0plt.plot([base_x, joint1_x, p2_x], [base_y, joint1_y, p2_y])
# 画出原点位置并以一个蓝色正方形表示
plt.plot(base_x, base_y, 'bs', markersize=15, label='Base')
# 画出节点1（joint-1）位置并以一个红色圆形表示
plt.plot(joint1_x, joint1_y, 'ro', markersize=15, label='Joint-1')
# 画出最终执行器的位置以一个绿色三角形表示
plt.plot(p2_x, p2_y, 'g^', markersize=15, label='End Effector')
# plot图的x， y坐标范围
plt.xlim(-100, 100)
plt.ylim(-100, 100)
plt.legend(fontsize=15)
plt.show()

以下为程序的输出，因为机械手的坐标是随机生成的，所以每次运行程序得到的图形都不会一样。



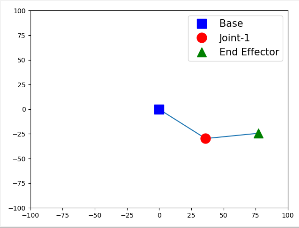
下面是compute_arm_config()函数的数学解释。



$x_1=l_{1}cos({\Theta }_1)$

$y_1=l_1\sin ({\Theta }_1)$

$x_2=l_{2}cos({\Theta }_1+{\Theta }_2)$

$y_2=l_2\sin ({\Theta }_1+{\Theta }_2)$

$x_2=l_{1}cos({\Theta }_1)+l_{2}cos({\Theta }_1+{\Theta }_2)$

$y_2=l_1\sin ({\Theta }_1)+l_2\sin ({\Theta }_1+{\Theta }_2)$

当我在编写程序时，我忘记了在第二个节点的位置需要加上第一个节点的角度,这个失误在以上的程序已经进行了更正。

2.广义坐标

同样的逻辑，计算一个2自由度机械手的末端执行器的位置可以应用到任何类似的n自由度系统的关节和链接约束到一个平面。对于每个新的关节/链接对，都要添加一定程度的自由度，并且需要一个额外的坐标来完整地描述系统的配置。

用于描述系统的瞬时配置(时间快照)的坐标通常称为广义坐标。“广义”一词指的是这样一种概念:对于任意的系统，这些角可以是角、x和y坐标，甚至是一些没有几何意义的其他量。

在前面的2自由度手臂示例中，所使用的广义坐标集由两个关节角组成。但是，也可以用其他的广义坐标，比如，第一个连杆的角度和末端执行器的x和y位置，或者关节和末端执行器的x和y位置。然而，在这些情况下，会有3和4个坐标，分别。这是因为关节和末端执行器的x和y位置不是独立的。它们通过固定链接长度(L)的约束相互关联

DoF =独立广义坐标个数

描述系统构型所需的独立广义坐标的个数等于自由度的个数。在2自由度机械手的练习中选择了两个特定的关节角度相对于一个特定的参考系，但是我们也可以很容易地选择其他角度相对于其他参考系。事实上，描述一个系统的广义坐标的可能选择数是无限的，但明智的选择是使用哪一组坐标最能简化需要解决的问题。

在串行机械手的机器人技术中，经常会遇到“位型空间（configuration）”或“关节空间(joint space)”这个术语，它指的是机械手可能具有的所有可能构型的集合。理解位型空间对于路径规划和避障非常重要。

3.空间坐标

一个刚体在空间坐标中具有六个自由度

• 位置（x, y, z）
• 角度（α,β,γ）

一个点在空间中具有3个自由度

• 位置（x, y, z）

4.节点连接类型

机构学运动副



如图所示，节点可以分为具有一个自由度（DoF）的低阶对和具有两个或三个自由度（DoF）的高阶对。用于串行操作器，最常见的关节类型是转动副和移动副，分别允许一个转动自由度和一个平移自由度。

出于建模目的，高阶对总是可以被低阶对的集合所取代，因此在不失一般性的情况下，我们可以将注意力仅限于转动副和移动副的1自由度的关节连接类型。



这里所示的系列机械手有n=3个关节:2个转动关节(圆柱)和1个移动关节(正方形)。每个关节连接两个连杆，所以连杆总数为n+1 = 4。注意,${\theta }_1$描述的转动连接地面和关节1和关节2之间的连杆上。因此，任意具有3个1自由度关节的串联机械手的自由度总数为:

$DoF=6（连接体的数量）-5（1自由度关节数量）$

=6（3）−5（3）= 6（3）-5（3）