本文是已读书籍的内容摘要,少部分有轻微改动,但不影响原文表达。
:以漫画形式来讲解最基本的统计概念和方法。
- ISBN: 9787121299636
- https://book.douban.com/subject/26906845/
2 - 探寻参数
2.1 - 中心极限定理(Central Limit Theorem)
概率分布曲线
想准确地预测变量,那么首先要了解目标变量的基本行为。
- 确定目标变量可能输出的结果,以及这个可能的输出结果是离散值(孤立值)还是连续值(无限值)。
- 为事件(值)分配概率:如果一个值不会出现,则概率为 0%。概率越高,事件发生的可能性就越大。
大量重复一个实验,并记录检索到的变量值,根据这些值作图,就可以得到一个概率分布曲线。
这个图表明目标变量得到一个值的概率,也就是该变量的概率分布。
理解了值的分布方式后,就可以开始估计事件的概率了,甚至可以使用公式(概率分布函数)。
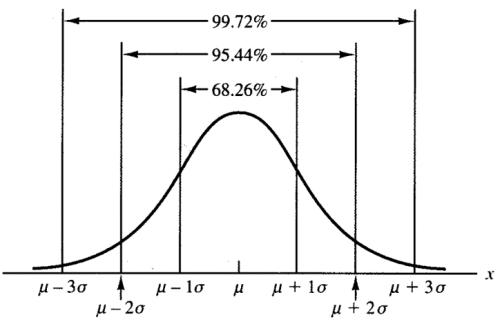
正态分布(Normal distribution)
也称为正态概率分布、“常态分布”、高斯分布(以著名数学家高斯的名字命名),是最常用的概率分布。
正态分布是只依赖数据集中两个参数的分布
- 平均值:样本中所有点的平均值。
- 标准差:表示数据集与样本均值的偏离程度。
如果对概率分布作图,将得到一条倒钟形曲线,样本的平均值、众数以及中位数是相等的,那么该变量就是正态分布的。
也就是说,只要用平均值和标准差就可以解释整个分布,因此预测任何呈正态分布的变量准确率通常都很高。
自然界和日常工作生活中的大部分变量都呈置信度为 x% 的正态分布(x<100),也就是说差不多都能用高斯分布描述。
中心极限定理
从某个总体中采集了一连串各自独立的随机样本。
算出每个样本的平均数。然后把这些平均数按顺序堆积起来。
堆在一起的平均数最终将开始聚集,随着堆放的样本平均数越来越多,堆放的外形就越来越接近正态,就像一个对称的古钟。
概括起来,中心极限定理说明的是在大样本条件下,不论总体的分布如何,样本的均值总是近似地服从正态分布。
可以简单的理解为:随机样本平均数倾向于聚集在总体平均数周围。
事实证明:
- 平均数堆成的大型数据堆的中心值等于产生样本的总体的中心值。
- 大型随机样本平均数堆往往比产生这个数堆的总体的外形更窄,以总体平均数为中心。具体程度取决于每个样本的大小。
- 样本大小越大,平均数堆积形状越窄。
特别注意:中心极限定理只有在每个样本均为随机抽取,且每个样本都足够大时才成立。
2.2 - 概率
概率是一个数值,用于对某个随机事件的长期可能性进行量化。
- 概率仅适用于长期,短期重来不会带来确信的结论。
- 每一个概率都有一个对立面,原因是所有概率之和永远是100%。
- 只能计算随机事件的概率,这也是总是随机采集统计值的原因。
2.3 - 推断
由于样本平均数倾向于聚集在总体平均数周围,可以用来猜测总体平及其大量样本平均数,以此画图显示出样本平均数的堆积形状。
也就是说,用一个随机样本,构建了一个估计抽样分布,然后用这个抽样分布算出置信区间。。
- 采集极大量样本平均数,以此画图,显示出样本平均数的堆积形状。
- 以中心极限定理为蓝图绘制图形,这张图叫做估计抽样分布。
- 估计抽样分布是一个估计结果,是在采集海量样本平均数后,对平均数分布情况的估计。
2.4 - 信心
不断采集更多随机样本,构建更多估计抽样分布,就会不断得到不同的区间。
如果用这种方法计算出极大量各不相同的区间,则大约有1/20样本不包含真正的总体平均数,19/20样本包含真正的总体平均数。
也就是说,有95%的信心来推断总体平均数就在这个范围内的某个地方,有5%的概率是错的。
事实上,从总体中随机采集的任何一个样本都有可能存在误导性。
如果一个样本存在误导性。那么基于这个样本构建的估计抽样分布也存在误导性。
但从长远来看,大多数随机样本平均数倾向于聚集在总体平均数的周围,这种采用估计和剪切的计算方法是有效的。
2.5 - 恨之深
依据如下要素,就可以构建一个估计抽样分布,然后剪去尾部,得到一个可靠的论断,包括一个置信水平和一个置信区间。
- 一个合理的英文大小
- 一个样本平均数
- 一个样本标准差
构建估计抽样分布的这个过程包括一系列数学运算,因此只能对用数字进行度量的特性成立。
对于明显不能用数字表示的特性,这个过程一般难以成立。
实际上,只要能够度量特性(创造一个数字尺度),并将这种度量结果记录在数轴上,就可以计算该特性。
根据单一样本得出的任何结论,都可能大错特错。
即使放大置信水平,涵盖更大区间,仍然有可能是错的。
2.6 - 假设检验
采用估计结果,然后把估计结果移到另一个中心位置,看看能得出什么结论,这个过程被称为假设检验。
目的是检验所设想的总体平均值的位置。
通过假设检验,将猜测值与样本中找到的平均数进行比较,以此检验猜测。
从长期看,期望所有样本平均数的95%都聚集在距离实际总体平均数两个标准差的范围内。
假设性检验的逻辑基础是在“假设条件”成立的情况下,取得当下样本的概率有多大,当概率足够小时就可以认为“假设条件”不成立。
比如,在“假设条件”成立的情况下得到当下样本的概率是5%,那就有95%的把握证明“假设条件”不成立。
简单地说,假设检验的基本思路和原理有两个:
- 一个命题只能证伪,不能证明为真。也就是说,个案当然不足以证明一个全称命题,但是却可以否定全称命题。
- 在一次观测中,小概率事件不可能发生证明逻辑:想要证明命题为真---》证明该命题的否命题为假---》在否命题的假设下,观察到小概率事件发生了,否命题为假---》命题为真。
举例说明
命题“A是合格的投手”
---》证明否命题“A不是合格投手”为假
---》观察到一个事件(比如A连续10次投中10环),而这个事件在“A不是合格投手”的假设下,概率为p(显著水平),小于0.05
---》小概率事件发生,否命题被推翻,也就是否命题“A不是合格投手”为假
---》原命题“A是合格的投手”为真
---》P值越小,说明这个事件越可能是小概率事件,否命题越可能被推翻,原命题越可信
2.7 - 破立之争
在假设检验的实践中。总是将一种设想与另一种设想进行比较。
假设检验往往包括两种相互对立的设想。
每一种设想各自为抽取到的数据来历做出了不同的解释。
假设检验的要点:断不可妄下结论。
第1步:问题是什么?
- 确定你要研究的问题是什么.
- 明确的问题,会帮助你批判性地筛选信息。
第2步:证据是什么?
- 找到与问题相关的证据。
- 向专家咨询意见,或求教过来人的经验,或查询相关的数据资料作为证据。
第3步:判断标准是什么
- 找到证据后,要判断证据是否有效,就需要一个判断标准。
- 这个判断标准要能够做到“不错过一个坏人,不冤枉一个坏人”的效果。
第4步:做出结论
- 根据找到的证据和判断标准,做出正确的结论。
- 这是一种使用数据和概率来做决策的过程。

3 - 走向高级
解决高级统计问题需要依靠各种各样的技巧。
重点在于,即使高级统计学技巧各种各样,无穷无尽。但统计推断的基本步骤保持不变。
本质上一切统计问题都相似,因此解决办法也雷同。
收集样本数据,估计出某种抽样分布,截取概率部分,有时候也需要把这个分布推移到一个新的位置,最后得出有信心的结论。