正规的语法特点
1.全部长度有限的语言都是正规的。
2.用正规文法当然能产生无限长串,当中周期反复部分的长度不大于非终止符的长度。
举个样例
在此规则之下。能生成句子
当中周期反复部分为ab,这个样例的非终止符的元素个数为2,故满足2不大于2.
自嵌入特性
我们把上下文无关文法中的正规文法去掉。剩下的那部分我们叫做真正的上下文无关文法。
自嵌入特性是区分真正的上下文无关文法与正规文法的判定标准。
即一个真正的上下文无关文法一定具有自嵌入特性。正规文法具有非自嵌入特性。亦即非自嵌入的上下文无关文法是正规文法。上下文无关文法就蜕化了。
什么是自嵌入特性?
自嵌入顾名思义,就是可以自己嵌入自己:
当然必须保证v和x不能是空串。
uvwxy定理
这是一个用以判定上下文无关文法和正规文法的条件。
就是说,当这个文法满足自嵌入条件,表示出来就是
那么,能够得到
当中当v和x的反复次数同样且为非空串时,则这个文法肯定就是真正的上下文无关文法。由于这样的周期形式是正规文法所不具有的。比方这样的
就是必需要用真正的上下文无关文法。
以下介绍上下文无关文法的等价文法。
不同的上下文无关文法。它们生成的语言有可能是等价的,这样就涉及到一个最优文法的问题。那么最优是什么?最有就是高效、没有冗余和浪费。
粗略说有2种冗余,并且仅仅有非终止符可以冗余。终止符总是实用的啦。
其一是浪费环节。
浪费环节是说由单个非终止符传递到了单个的非终止符。比方
这样的形式意味着B是多此一举的。还不如直接A到C呢。
其二是无用环节。
细分又有2类。
通俗说
1.无尾的无用非终止符
所谓无尾,就是咱用了这个终止符,话根本都没法结束。
有头无尾。
A根本没法最后变成常量(终止符)。
不存在x使得
2.无头的无用非终止符
所谓无头,就是这句话根本就不可能从这个非终止符開始。有尾无头。
从起始符開始根本找不到含有A的句子。
从起始符S開始,不存在
首先介绍怎样消去浪费环节。
消去浪费环节包含2个部分。
其一消去。
其二修正。
消去过程
这个过程用递归算法来实现。
就是要求出全部非终止符各自相应能到达的全部非终止符集合。
举个样例就好了
如今消去浪费环节,先考虑S。
发现S能在一步之内的非终止符仅仅有A
记
在K1(S)集合中再次出发。在一步之内能走到的新非终止符仅仅有B
记
再往后没有新的非终止符了。
同理考察A,A在一步之内能到达的非终止符仅仅有B了,记
再考察B,B根本就没有能在一步之内能到达的新终止符。
于是这相应的3个集合就求完了
修正过程
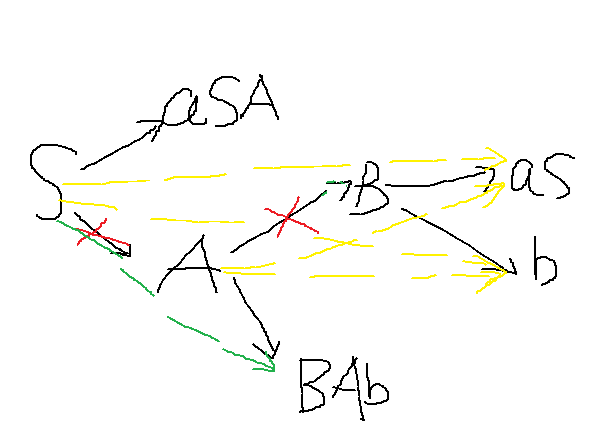
修正过程就依照上面的消去过程打补丁就好了,由于要消去一堆连接。旧桥拆了总得又一次修吧。还是上面那个样例,先把之前的生成关系画出来,如图1黑线所看到的。
图1
如今考虑A,依据集合,我们要去掉A到B的连接
那么就得补上S到b、A到b、S到aS、A到aS。黄线代表。
然后再考虑S。要去掉S到A
那么就得补上S到BAb。绿线代表。
注意:如今尽管看起来文法规则比曾经更麻烦了,可是,实际生成句子的过程却变得简单了很多,所以简化没简化还是要看疗效。
以下介绍消去没用的终止符
消去无用终止符的思路就是。找出全部实用的非终止符,那么剩下的自然就是没实用的了。
消去无尾非终止符
找出全部的有尾非终止符集合。定义为J(G)
方法是
这个表达式非常清晰。还是举个样例。反而绕口。但还是举吧
这个表达式事实上是一步步找到那些终于的到达终止符的非终止符。
首先J0(G)为空集。
则J1(G)为全部能一步走到以终止符为尾的非终止符,即A
继续,J2(G)是J1(G)并上全部能在一步之内到以J1(G)或者其它终止符为尾的非终止符。
好绕口。。。
事实上就是{S,A}
再往下就找不到了。只是如今忽然发现,B呢?怎么没看到B的影子。
这就说明B就是无尾的无用非终止符。
去掉全部跟B有过关系的生成关系就好。如今是新的生成关系
再说说消去无头非终止符
也是仅仅要找出全部有头的非终止符就好。剩下自然就无头了
用表达式表示是这种
这个表达式的意义事实上就是从起始符,回溯一步步展开,希望能找到句子的头部。
还是举个样例
展开起始符S,发现S能到aAA,因此R1(S)={S,A}
A继续展开。发现A能到aCA。因此R2(S)={S,A,C}
搞定,又发现原来B是无头的非终止符,赶紧删掉与它有关系的全部表达关系就好了。不再赘述。
上下文无关文法的2中标准型
1.C(Chomsky)标准型
举一个样例马上就知道怎么把随便一个上下文无关文本变成C标准型了:
2.G(Greibach)标准型
这个严格的转化方法有点畸形,就临时不展开了。
简单情况用凑的就好了。
欢迎參与讨论并关注本博客和微博以及知乎个人主页,兴许内容继续更新哦~
转载请您尊重作者的劳动,完整保留上述文字以及本文链接,感谢您的支持!
版权声明:本文博客原创文章,博客,未经同意,不得转载。