java 二分搜索获得大于目标数的第一位_程序员常用查找算法(顺序、二分、插值、分块、斐波那契)...
顺序查找
基本思想
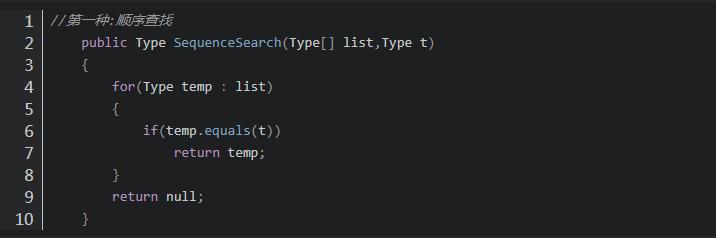
属于线性查找和无序查找,从一端开始顺序扫描,直到找到与目标值value相等的元素。
这是最基本的查找方法,也是时间复杂度最高的查找算法。
在数据过多时,这种方法并不适用。
代码实现
分块查找

基本思想
属于顺序查找的改进方法,又叫索引顺序查找。
将n个元素分成m块(m<=n),每个块中元素可以没有顺序,但是m个块之间是有序排列,所以特别适合于节点动态变化的情况。
分块查找的速度虽然不如二分查找算法,但比顺序查找算法快得多,同时又不需要对全部节点进行排序。当节点很多且块数很大时,对索引表可以采用折半查找,这样能够进一步提高查找的速度。
那么索引表的构成就是每个块中的最大元素。
查找方式是先对索引表进行二分或顺序查找,选出目标值应该所在的块,然后在块内进行顺序查找。
二分查找

基本思想
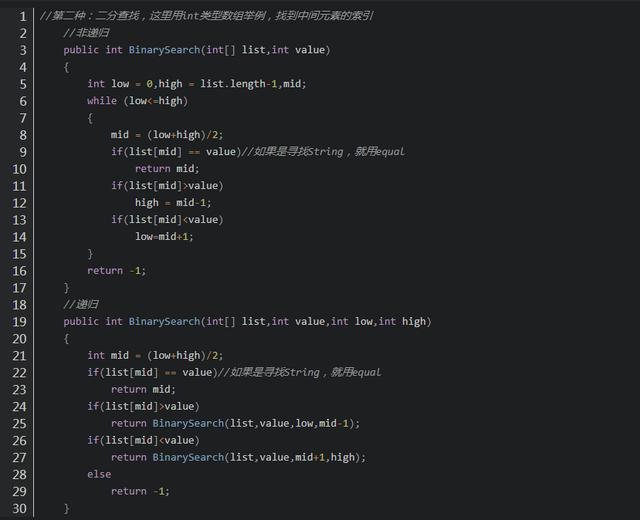
属于有序查找算法,也叫折半查找,就是将数组每次选取一半进行查找,怎么选取一半就需要让中间值与目标值value进行比较,因为有序,所以中间值小于目标值则选取后半部分,大于目标值则选取前半部分,依此类推,直到找出与目标值相等的元素,否则返回-1或null。
这种方法有效的缩减查找次数和查找范围,适用于数据量比较大的有序表。
因为前提是有序表,所以对于插入删除等操作过多的数据集并不适用,因为在排序算法上浪费的时间会比较多。
一般的时间复杂度是O(log2n)
代码实现
插值查找
基本思想
属于二分查找的改进版,二分查找一直重复一半一半的操作,这种操作比较固定,并不会根据目标值的大小进行自适应分段和选择,而插值查找可以根据目标值value进行自适应。
下面是百度词条对插值的解释:插值类似于平常查英文字典的方法,在查一个以字母C开头的英文单词时,决不会用二分查找,从字典的中间一页开始,因为知道它的大概位置是在字典的较前面的部分,因此可以从前面的某处查起。
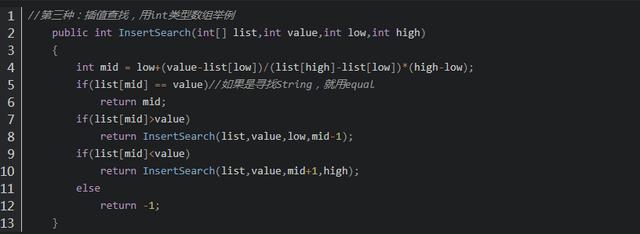
既然是二分查找的改进版,那么就要找关键点进行改进,二分是取1/2的有序表进行查找,那么mid就是关键点,二分中mid=(low+high)/2,可以转化成mid=low+(high-low)/2,所以相当于(high-low)/2中的1/2就是所分的比例,那么可以对mid进行改进,mid=low+low+(value-list[low])/(list[high]-list[low])*(high-low),(value-list[low])/(list[high]-list[low])就是所分的比例。
根据目标值在整个有序表中所处的位置,让mid的变化更靠近目标值value,这样也就间接地减少了比较次数。
这种方法适用于关键字分布均匀的有序表。
复杂度为O(log2(log2n))
代码实现
斐波那契查找
基本思想
斐波那契数列与0.618有着奇妙的关联,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,所以可以将黄金比例运用到查找中。
百度词条:斐波那契搜索,斐波那契搜索就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F(n),将原查找表扩展为长度为F(n)(如果要补充元素,则补充重复最后一个元素,直到满足F[n]个元素),完成后进行斐波那契分割,即F[n]个元素分割为前半部分F[n-1]个元素,后半部分F[n-2]个元素,找出要查找的元素在那一部分并递归,直到找到。
这个方法比较重要,所以百度词条上讲的很清楚!
代码实现
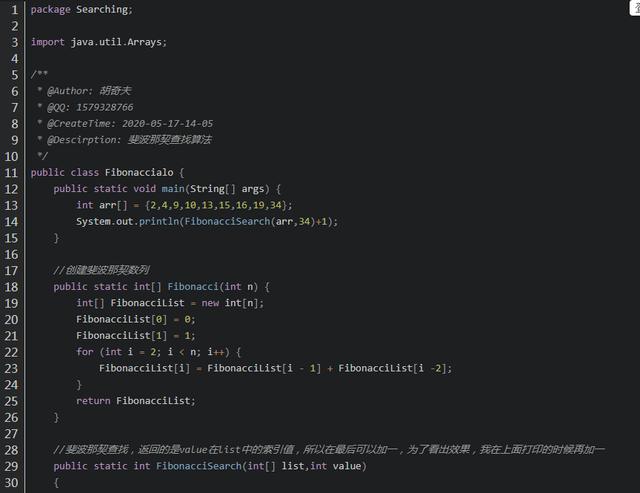
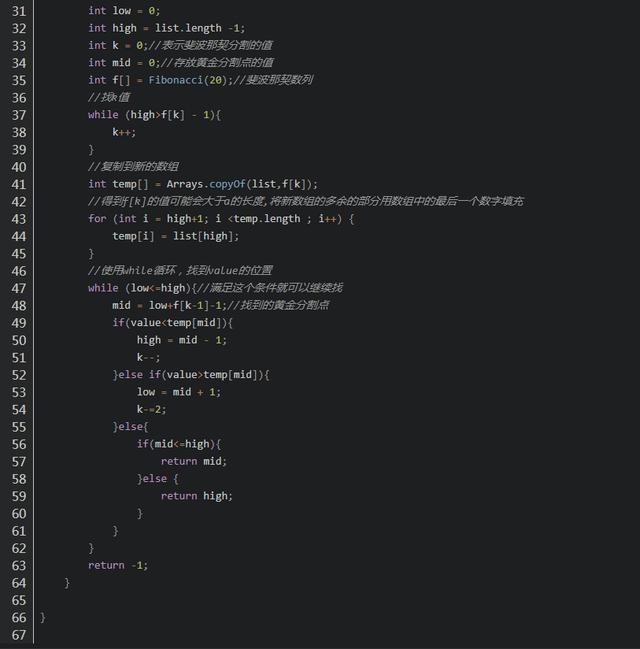
总结
- 还剩下两种非常重要的查找算法,就是树表和哈希,这两种我就单独写,ball ball大佬们不要嫌弃!
更多相关:
-
注:本文内容参考《35 Practical Examples of Linux Find Command》 网址:http://www.tecmint.com/35-practical-examples-of-linux-find-command/ Linux 查找命令是Linux系统中最重要和最常用的命令之一。查找用于根据与参数...
-
find 按时间查找 转载▼ 分类: linuxShell日记 -mtime 修改时间-ctime 改变时间-atime 访问时间-mtime +5 至少5天之前修改过的文件,至少5天没修改过-mtime -5 5天之内修改过的文件-mtime 5 刚好5天前修改的文件 -perm 按权限查找 -perm 001 精确...
-
前两篇 《程序员必知8大排序3大查找(一)》 《程序员必知8大排序3大查找(二)》 三种查找算法:顺序查找,二分法查找(折半查找),分块查找,散列表(以后谈) 一、顺序查找的基本思想: 从表的一端开始,顺序扫描表,依次将扫描到的结点关键字和给定值(假定为a)相比较,若当前结点关键字与a相等,则查找成功;若扫描结束后,仍未找到...
-
Find从英语字面上的意思译过来是发现,找到的意思,它在linux中作为文件查找命令也十分形象,Find虽说只是个命令,但其功能非常强大。 好,下面来说说Find,先来说说它的基本语法格式:find [查找路径] [查找标准] [处理动作]查找标准: -name 文件名称查找 ...
-
栈stack:stack 后入先出(LIFO) q.top()获取栈顶元素(并不删除)q.pop()删除栈顶元素q.push(x)向栈中加入元素q.empty()判断栈是否为空 队列queue:先入先出(FIFO) q.front()获取队首元素(并不删除)q.pop()删除队首元素q.push(x)向队列中加入元素q....
-
resize(),设置大小(size); reserve(),设置容量(capacity); size()是分配容器的内存大小,而capacity()只是设置容器容量大小,但并没有真正分配内存。 打个比方:正在建造的一辆公交车,车里面可以设置40个座椅(reserve(40);),这是它的容量,但并不是说它里面就有了40个座椅,只能说...
-
v-for="(index,$i) in total" :key="$i":style="{left:`${itemWidth*((index-1)%rowItemCount)}px`,top:`${itemHeight*(Math.ceil(index/rowItemCount)-1)}px`}" //total是显示总数量 //l...
-
技巧一(推荐指数★★★★★) 采用top、right、bottom、left,可以不在乎父元素的宽度和高度,对GPU损耗低于技巧三,但是对浏览器内存的消耗高于技巧三 .子元素 {/*父元素需要position: relative|absolute;*/position: absolute;margin: auto;to...
-
设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。 push(x) – 将元素 x 推入栈中。pop() – 删除栈顶的元素。top() – 获取栈顶元素。getMin() – 检索栈中的最小元素。 示例: MinStack minStack = new MinStack(); minStack...
-
注意,前情提示: 本代码基于《Node.js(nodejs)对本地JSON文件进行增、删、改、查操作(轻车熟路)》 传送门Node.js(nodejs)对本地JSON文件进行增、删、改、查操作(轻车熟路)_你挚爱的强哥❤给你发来1条消息❤-CSDN博客 在/api/demo/文件夹下面创建CURD.js...
-
第一:在map端产生join mapJoin的主要意思就是,当链接的两个表是一个比较小的表和一个特别大的表的时候,我们把比较小的table直接放到内存中去,然后再对比较大的表格进行map操作。join就发生在map操作的时候,每当扫描一个大的table中的数据,就要去去查看小表的数据,哪条与之相符,继而进行连接。这里的join并不会涉...
-
** 0x01 原理分析 ** 还是很早之前爆出来的漏洞,现在拿出来学习一下,参考阿里巴巴:https://security.alibaba.com/... 漏洞发生在/inc/common.inc.php页面中。首先看这个函数: 首先使用ini_get来获取php.ini中变量'register_globals'的值,而r...
-
就之前本人主持开发的金融产品所遇到的安全问题,设计部分请参见:http://www.cnblogs.com/shenliang123/p/3835072.html 这里就部分web安全防护就简单的交流: 1.1系统安全 1.1.1 客户端脚本安全 (1)跨站脚本攻击(XSS): XSS攻击,通常指黑客通过“html注...
-
一、活动目录灾备简介 本次演练我们将讨论如何让域控制器从灾难状态(例如由于硬件或软件故障引起的数据库故障)进行恢复的步骤。此类灾难通常会导致域控制器失效,而且会使计算机无法正常引导;将只提供对运行 Active Directory 的域控制器(不运行其它服务)进行恢复的信息。如果该计算机上还安装有其它服务,例如域名系统 (DNS)...