题目地址
题目链接
题解
动态主席树的板子题。动态主席树其实和静态的有很大差别,虽然同样是n个根,但是节点并不能共用,每个根节点表示bit上的一段区间。
所以其实是个树套树的东西来着,外层是bit,内层是主席树。
然后将所有数离散(包括读入进来的修改的数,所以动态主席树其实是离线的),那么就映射成了一段连续区间,用主席树维护这段区间。
每次修改就把x->n(+=lowbit(x))的所有节点的数v的那条链加上v,注意动态开点,不然空间爆炸。这样子 空间就是 (nlog^2n)的(每次修改只会动到一条链,一共动log条,所以是(log^2)的)。可以看一下下面这个图,很形象。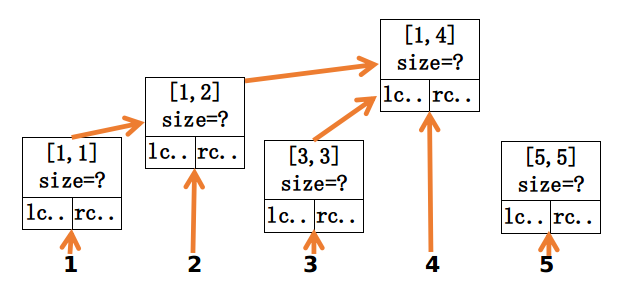
(图片来源于Flash_Hu)
每次查询将l-1和r两个点的前缀和在bit上面对应的节点找出来(log个),然后在主席树上向下走,一次同时减l-1对应的log个主席树,同时加r对应的log个主席树。
这样子时间复杂度是(O(nlog^2n))。
大概就是这样...然后查询可以写成类似二分的写法,就可以非递归找了。但是修改还是写成递归的靠谱一点(非递归要写指针,指针容易写挂..)。还有注意每次修改要修改的是离散化后的值,但是输出要输出离散前的。
再看个代码意会一下应该就没问题了...
#include
using namespace std;
typedef long long ll;
const int N = 200100, M = 40000100;int a[N], b[N], len;
int l[N], r[N], op[N], d[N];
int n, m, root[N], rootl[30], rootr[30], tot;
struct tree {int lc, rc, sum;
}t[M];#define lowbit(i) (i&(-i))
void upd_tree(int &rt, int l, int r, int pos, int v) {if(!rt) rt = ++tot; t[rt].sum += v;if(l == r) return;int mid = (l + r) >> 1;if(pos <= mid) upd_tree(t[rt].lc, l, mid, pos, v);else upd_tree(t[rt].rc, mid + 1, r, pos, v);
}void upd(int pos, int k, int v) {for(int i = pos; i <= n; i += lowbit(i)) {upd_tree(root[i], 1, len, k, v);}
}
#define lc(i) (t[i].lc)
#define rc(i) (t[i].rc)
int query(int L, int R, int k) {int sum = 0, cur_l = 0, cur_r = 0;for(int i = L - 1; i; i -= lowbit(i)) rootl[++cur_l] = root[i];for(int i = R; i; i -= lowbit(i)) rootr[++cur_r] = root[i];int l = 1, r = len;while(l != r) {int mid = (l + r) >> 1; sum = 0;for(int i = 1; i <= cur_r; ++i) sum += t[lc(rootr[i])].sum;for(int i = 1; i <= cur_l; ++i) sum -= t[lc(rootl[i])].sum;if(k <= sum) {r = mid;for(int i = 1; i <= cur_l; ++i) rootl[i] = lc(rootl[i]);for(int i = 1; i <= cur_r; ++i) rootr[i] = lc(rootr[i]);}else {l = mid + 1, k -= sum;for(int i = 1; i <= cur_l; ++i) rootl[i] = rc(rootl[i]);for(int i = 1; i <= cur_r; ++i) rootr[i] = rc(rootr[i]);}}return b[l];
}
#undef lc
#undef rcint main() {scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++i) scanf("%d", &a[i]), b[++len] = a[i];for(int i = 1; i <= m; ++i) {char ch[5];scanf("%s%d%d", ch, &l[i], &r[i]);op[i] = ch[0] == 'Q';if(op[i]) scanf("%d", &d[i]);else b[++len] = r[i];}sort(b+1,b+len+1); len = unique(b+1,b+len+1)-b-1;for(int i = 1; i <= n; ++i) a[i] = lower_bound(b+1,b+len+1,a[i])-b;for(int i = 1; i <= n; ++i) upd(i, a[i], 1);for(int i = 1; i <= m; ++i) {if(!op[i]) {upd(l[i], a[l[i]], -1);a[l[i]] = lower_bound(b+1,b+len+1,r[i])-b;upd(l[i], a[l[i]], 1);} else {printf("%d
", query(l[i], r[i], d[i]));}}return 0;
}