7.非理想情况

（1）积分饱和

到目前为止，我们一直使用的“理想”形式的PID控制器很少用于工业中。“时间常数”形式更为常见。

当前说明了理想形式的一些重大缺陷。

在一个经过良好调整的系统中，积分项能够通过使控制作用力与累积误差成比例来消除稳态误差。然而，这种操作模式会带来危险。设想，如果设定值突然大幅度改变但系统动力学相应缓慢。例如，如果当前房间的温度为50°F（10°C），然后将恒温器上的设定值移至75°F（24°C）。加热系统可能需要数十分钟来将温度驱动到所需的设定值。直到跟踪误差为零，积分项将继续增长（即“饱和”），故名积分饱和。

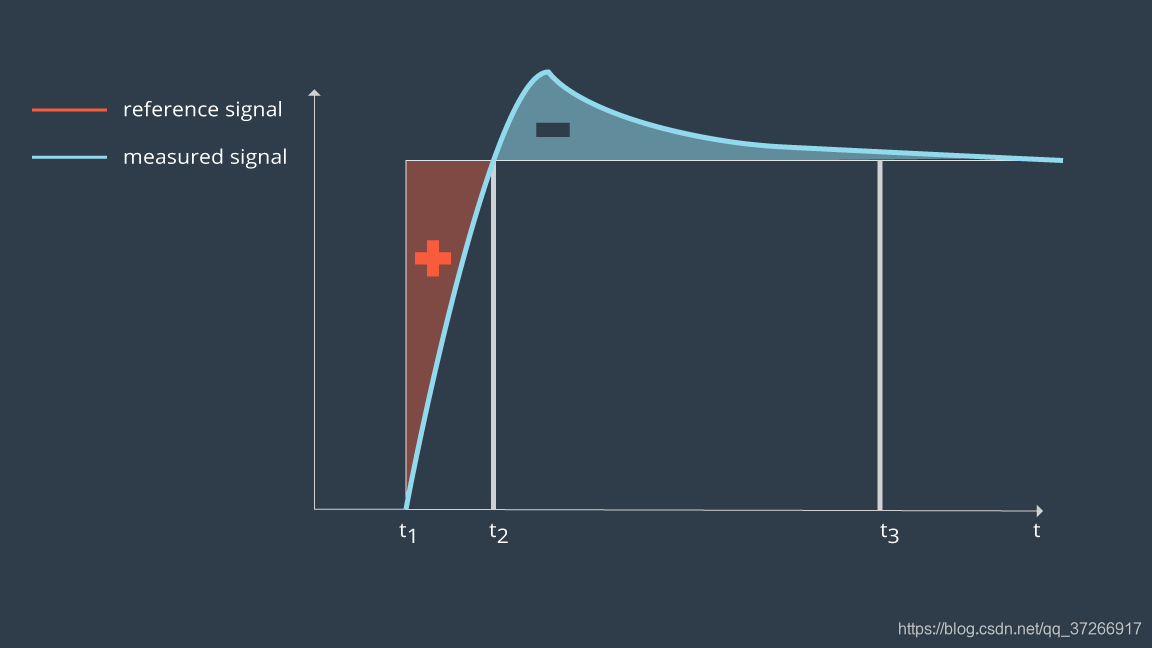由于累积的误差和缓慢的系统动力学，即使达到设定点，控制器仍将继续运行熔炉（提高温度），从而导致较大的过冲。然后，系统将花费时间来“消除”累积的误差，然后再次达到所需的设定点。

可能导致积分饱和的另一种情况是由于执行器饱和。如果将设定点更改得足够远，则即使执行器以100％输出（即饱和）运行，系统也可能永远无法达到期望的目标。唯一的希望是将设定值提高到可以达到的水平。

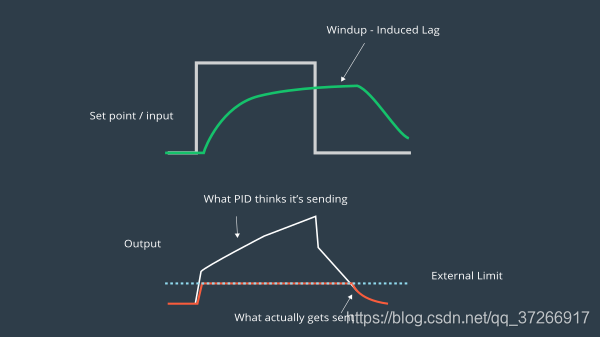已经设计了许多策略来解决积分饱和。一个简单的方法是在控制器输出完全饱和时停止对误差进行积分。

（2）噪音

大多数PID控制器实际上只是PI控制器， 那么微分增益可能带来哪些问题？

想象一下，四轴飞行器徘徊在所需的高度，但是由于有风，所以飞行器上下颠簸。

$$\frac{de}{dt}\approx \frac{e-e_{old}}{\Delta t}$$

此处显示了导数的有限差分形式的方程式，其中$\Delta t$是一个很小的数字，可能在毫秒或微秒的数量级，最终结果是扩大差异。

在实践中，这会在存在高频噪声的情况下造成严重的问题，因为控制器认为空气信号发生了很大变化，并且做出了巨大的控制努力。

虽然可以添加一个低通滤波器来消除一些高频噪声，但是这样做确实会降低微分控制的性能，因为它依赖于对空气变化率的响应。通常，需要大量的实验来平衡效果来获得令人满意的性能。

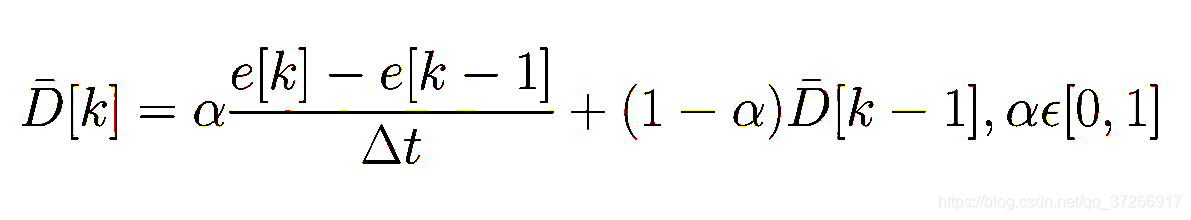
低通滤波器的一个简单实现是一阶递归滤波器，其中$\alpha$是平滑因子。$\alpha$越小，抑制的高频噪声就越多，这增加了控件设计者必须选择的另一个参数。

此外，递归滤波器还增加了滞后。即，它延迟了控制器向系统的输入，使系统更难控制。但是，由于此滤波器仅使用一个先前的输出值来计算当前值，因此延迟的影响通常是比较小的。

编写一个低通滤波器

import numpy as np
import matplotlib.pyplot as pltf1 = 5  # Hz
w1 = 2*np.pi*f1  # 角频率
f2 = 50  # Hz
w2 = 2*np.pi*f2  # 角频率# 创建一个时间点数组
N = 500
t = np.linspace(0, 5, N)# 创建信号
pure = np.sin(w1*t)  # 纯正弦波
noise = np.sin(w2*t) + np.random.normal(0, 0.2, N)  # 正态分布随机噪声
# 0   = 正态分布的均值
# 0.2 = 正态分布的标准差
# N   = 数组中元素的数目
signal = pure + noise  # 嘈杂的正弦波# 递归低通滤波器
alpha = 0.01  # 接近零意味着更强的平滑效果filtered = np.zeros(N)  # 初始化数组以存储值
for i in range(N):if i > 1:# 用低通文件的代码填写过滤的[i]变量filtered[i] = alpha * (signal[i] - filtered[i-1]) + filtered[i-1]fig = plt.figure()
ax1 = fig.add_subplot(311)
ax1.plot(t, pure)
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Amplitude, (m)')
ax1.set_title('5 Hz, Pure Signal')ax2 = fig.add_subplot(312)
ax2.plot(t, signal)
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Amplitude, (m)')
ax2.set_title('Noisy Signal')ax3 = fig.add_subplot(313)
ax3.plot(t, filtered)
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Amplitude, (m)')
ax3.set_title('Filtered Signal')plt.tight_layout()
plt.show()

输出如下：

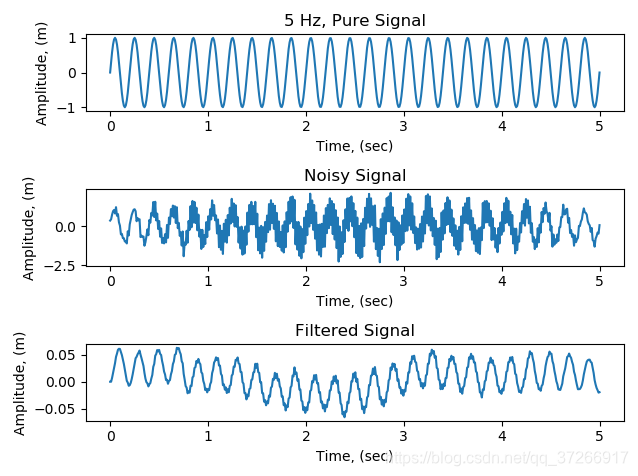
8.控制设计目标和准则

（1）控制器的主要目标

1. 稳定性。首先，控制器应提高系统稳定性。实际上，有很多方法可以定义和表征稳定性。适用于线性系统的一个常见定义是缩写BIBO。BIBO代表有界输入，有界输出，它表示只要输入低于某个值，那么输出就可以保证也低于某个值。更为严格的定义称为渐近稳定性。如果给出有限的输入或初始条件，则渐近稳定的系统可以保证收敛到固定的有限值（例如，落下的球最终将落在地面上）。显然，这对于现实世界的系统而言是非常理想的属性。

2. 跟踪。跟踪性能也很重要。跟踪是指控制器跟踪或保持参考输入信号的能力。参考点和实际输出之间的差异是跟踪误差。跟踪任务的一个示例是建筑物中的供暖和空调系统。可以通过恒温器设置所需的温度，该恒温器具有集成的传感器以测量当前温度，如果出现跟踪错误，恒温器将激活加热器或空调以将温度推向设定值。

3. 鲁棒性。正如统计学家乔治·博克斯（George Box）曾经写道：“所有模型都是错误的，但有些模型是有用的。”理想情况下，控制器将不会依赖于参数非常精确的非常详细的数学模型。

4. 干扰抑制。噪声和其他测量误差会破坏所有实际系统。虽然尝试并限制不想要的干扰很重要，但设计可容忍干扰的控制器也很重要。

5. 最优性。尽管不是每个控制器都需要，但在许多情况下，优化系统的某些属性非常重要，例如，最小化控制工作，在给定时间间隔内最大化行进距离或最小化跟踪误差。最佳控制需要系统的数学模型，设置控制输入上限和下限的约束方程式以及成本函数。梯度下降 /上升算法是优化成本函数的流行首选方法。

（2）控制器设计流程

成功的控制器依赖于系统的，多步骤的设计过程。大致而言，步骤为：

1. 确定系统的性能规格（例如，最大跟踪误差，超调百分比，建立时间等）
2. 如果可能，开发一个简单的系统数学模型 选择传感器和控制器类型
3. 设计控制器符合性能规格
4. 如果可能，请使用仿真来测试控制器性能
5. 选择硬件/软件来实施控制器
6. 在线调音控制器

控制器的目标是促进稳定性，跟踪性，鲁棒性和抑制干扰，但是现在的问题是，“控制信号$u(t)$应该如何起作用才能实现这些目标？”显然，为了最大程度地减小跟踪误差，控制信号应该是误差的一部分，但是它到底是什么样的呢？

可以断定，$u(t)$应该与误差的大小有关。换句话说，较小的误差应产生较小的控制输入，反之亦然。误差$e(t)$也很重要最终应该变为零，或者至少可以接受的程度。

另一个相当直观的属性是控制输入的变化不应太快。想象一下，如果巡航控制器只能通过完全打开或完全踩下油门和刹车来调节速度，那么旅程将是多么令人不愉快。快速或不稳定的输入至少有可能在执行器上造成不必要的磨损，并可能降低稳定性。最后，如果控制信号不依赖于了解特定的模型参数（例如汽车的质量，空气阻力系数或地形坡度），那将是有益的。

9.调优策略

到目前为止，重点是了解比例误差、积分误差和导数误差的主要影响。现在把我们的注意力转移到更系统的方法来选择PID增益。

多年来，提出了许多不同的参数调优规则和指导原则。一些最古老和仍然被广泛引用的技术是Ziegler-Nichols (ZN)方法。

齐格勒和尼科尔斯发表了与PID控制调谐相关的最有影响力的论文之一，这篇论文的题目是《自动控制器的最佳设置》。

从准确性和简洁性的角度来看，研究自动控制的纯数学方法无疑是最理想的方法。

然而，不幸的是，控制的数学涉及如此令人困惑的指数函数和三角函数的组合，以至于一般的工程师没有足够的时间来钻研这些函数来解决当前的问题。

为了帮助实践控制工程师，齐格勒和尼克尔斯发表了两个经验推导的方法，可以用于PID调整过程，至少作为一个起点。这些规则很容易遵循，涉及到一个系统的过程，并且对于许多系统都足够有效，这一事实无疑对这些方法的流行起了很大作用。

尽管Z-N方法不再被认为是“行业标准”，但是有必要熟悉一下它们，因为它们仍然经常遇到，而且许多现代调优指南是原始调优指南的变体。对调优方法的一些批评是:

(1)建议的增益基于来自系统对测试输入的响应的信息太少，

(2)容易产生太多的超调，

(3)跟踪性能差。

ZN方法1

假设:

1. 该装置对阶跃输入有s形响应。(或称，一阶加死区时间模型)，
2. 是开环稳定的。
   
   
   
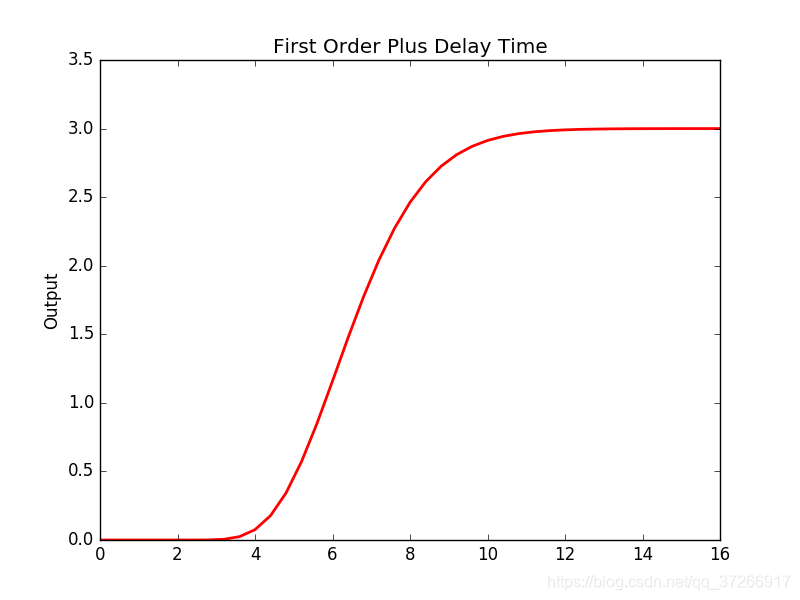
   ZN方法1的目标是实现良好的干扰抑制，他们将其定义为具有“四分之一衰减比”的系统响应(即，第二次超调峰值的振幅除以第一次超调峰值的振幅= 1/4)。

ZN方法2

假设:

1. 该系统是一个高阶系统，在闭环系统中，只采用比例控制就可以使系统达到稳态振荡

第二种方法的目标是实现具有25%超调的闭环阶跃响应。

这两种方法都假设PID控制器具有以下形式，

$$u(t)=K_p(e(t)+\frac{1}{{\tau }_i}{\int }_0^{t}e(\tau )d\tau +{\tau }_d\frac{de(t)}{dt}$$

其中

$${\tau }_i=\frac{K_P}{K_I}{\tau }_d=\frac{K_D}{K_P}$$

简单的手动调整

在许多情况下，简单的手动调整可以提供相当好的性能。可以通过以下方式开始：

1. 将Kp设置为小且Ki = Kd = 0，
2. 缓慢增加Kp以减少上升时间，
3. 缓慢增加Kd以减少过冲和稳定时间。

通过“手动”调整增益，系统响应越快，稳定性越差。反之亦然。诀窍是要在两者之间找到平衡。但是，使用上述方法找到近似解通常可以作为更系统的调整方法的起点，我们将在下面讨论的梯度下降算法。

10. 梯度下降算法（“Twiddle”）

一种更常的方法是使用梯度下降算法，有时也称为“Twiddle”。前提是要从三个增益的初始猜测向量开始。通常建议为P设置一个小的非零值，为I和D设置一个零。然后，分别对每个收益进行小幅更改，然后测试成本函数是否降低。如果是这样，将沿相同方向不断更改参数，否则尝试沿相反方向调整参数。如果增益值的增加或减少都不会降低成本函数，则可以减小增益增量的大小并重复。整个循环应继续进行，直到增量大小降至某个阈值以下。