首页 > msdn画圆弧函数_复变函数与积分变换 简明笔记(八)：保形映射（共形映射）

msdn画圆弧函数_复变函数与积分变换 简明笔记(八)：保形映射（共形映射）

11aab01d9f42b9a62384170251f09493.png

在第一部分中我们就引入了复变函数的概念，但由于复变函数是二维点集之间的映射，所以作出复变函数的图像并不简单。事实上，研究复变函数的图像性质，主要是观察它将

平面上的平面图形映成
平面（
）上的什么图形——也就是研究两个平面之间的图像的大小、方向、形状之间的关系。

在这一章的内容中，不必太过纠结代数上的严谨性和证明的完备性。即使前面的章节中有关复变函数的分析性质掌握得并不好，也不影响我们研究复变函数的图像作用效果。对定理和映射函数的直观作用效果的理解要比证明定理和命题更重要，在学习这一章的时候切记要转换学习思路。

我们需要理解的是如下的导数的几何意义：

考虑

，即原象区域内的一小段线段（研究线段是因为所有的曲线都可以看作是微小的线段组合成的结果），则
为这一小段线段的象。联想微分
，可以知道：从原象到象的映射
，它的导数
决定了从原象映射的结果。


这可以从
两侧取幅角和模得到：


(1)式表明
线段相比
线段
逆时针转过了
角度，


(2)式表明
线段相比
线段缩放了
的长度。

这两点还可以归结为一个定理：

设函数

在区域
内解析，
为
内一点，且
，则映射
在
具有：

(1) 保角性——在点

处两条曲线的夹角与映射后两条像曲线在像点
处的夹角保持大小和方向不变。（规定
是为了保证导数的幅角有意义，不然在
中会出现无意义的结果）

(2) 伸缩率不变性——过点

的任意一条曲线在
附近都会按
的比例缩放。

如果

在区域
内的每一点都具有保角性和伸缩率不变性，则称
是
内的保角映射。

注意上述框中的旋转角方向，如果为逆时针，则称

是第一类保角映射，如果为顺时针，则称
为第二类保角映射。通常来说，一个第一类保角映射函数的共轭，即为第二类保角映射。

此外，为了讲述这一章内容的方便，我们还需要记住以下几个具有指导意义的定理。这些定理不需要掌握证明，我们的应用也仅仅只停留在对这些定理的字面理解上。

（1）（逆映射的存在性）如果

能够把区域
保角地、一一对应地映射成区域
，则其反函数能够把
保角地、一一对应地映射成区域
。并且，
及其反函数可由此推得是单值且解析的函数。

（2）（黎曼定理，映射的存在与唯一性）如果有两个单连通区域

和
，
和
是其中两点，
是任一
之间的实数，则
总存在一个函数
，能够把
一一对应地保角地映射成
，使得
，并且这样的映射是唯一的。

（3）（边界对应原理）设单连通区域

和
的边界分别为简单闭曲线
和
，如果能找到一个在 内解析，在
上连续的函数
，它将
一一对应地映射成
，且当原象点和象点在边界上绕行方向一致时，
和
在边界的同一侧，则
将
一一对应地保角映射成
。

上述的定理（1）、（2）保证了映射的存在、唯一和可逆性，为寻找映射提供了理论依据。

定理（1）启发我们：要找

和
之间的映射，不必死盯着这两个区域看——不妨把它们都映射成某一标准图形，然后利用求反函数的方式来求这两个区域之间的映射。例如，将 和 都映射成为单位圆，从而可以知道， 和 之间存在某一个映射关系是： -单位圆- 。其中，从单位圆到 的映射由 到单位圆映射的逆映射来确定。

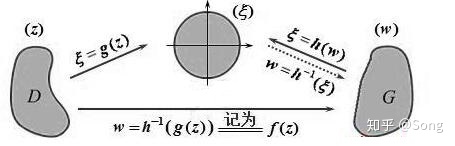
b5872d8c0f41a0007cb17183bd45cc08.png

从（2）中我们可以知道，给定原象区域、像区域、映射的对应两点和旋转角，就可以唯一确定两个区域间的一一映射——但这对“如何寻找”没有帮助。

而定理（3）则告诉我们：只需要盯着这两个区域边界上的一些点就可以帮助我们确定这个映射的具体形式了。

这一章的内容过于广泛，所以我们只研究一种简单并且重要的保角映射：分式线性映射。

分式线性映射定义为

。括号中的限制是为了保证映射的保角性，否则
，整个
平面会被映成
平面上的一点。为了能够让无穷远点也被包含在这个映射中，
我们讨论的保角映射是定义在扩充复平面上的。所以对于上式需要补充定义：

当

时，在
处定义
；在
处定义
;

当

时，在
处定义
.

另外，需要再次强调的是，无穷远点仅为保证分式线性映射而引入，其模、幅角均无意义。

有了分式线性映射的定义，我们不加证明地叙述分式线性映射的直观作用效果。

1. 保圆性

保圆性指分式线性映射将

扩充复平面上的圆映射成
扩充复平面上的圆。但需要注意是，“圆”指的并不止是平面上到定点为定距离的点集。由于引入了扩充复平面，圆可以通过无穷远点——在这种情况下，圆的半径会变为无穷大，此时它表现为一条直线。所以准确地来说，如果 扩充复平面上的圆（或直线）上的某点被映射成了无穷远点，那么
扩充复平面上的圆将会变为直线，否则，它将映射成为半径有限的圆周。

2. 保对称点性

保对称点性指：如果分式线性映射将圆周

映射成圆周
，则它能够将关于
对称的两点
映射成关于
对称的两点。

如果

是直线，则映成关于直线对称的两点。

此处“关于圆周对称”的定义为：若

关于半径为
的圆心为
的圆对称，则
。其几何意义如图所示。在复变函数中，为了沿用此定义，我们还补充定义：原点
和无穷远点关于单位圆对称。在这门课中，有关这条定义特别我们需要记住的只有：
和
关于单位圆
对称；
关于实轴对称。

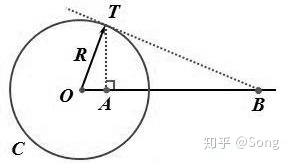
61d7c714599a7dd8d9f039e91212c821.png

在解决实际问题中，我们通常只需要用到保角性+保圆性+边界对应原理，即可解出需要的分式线性映射的形式。对于

，分子分母上下同时约去一个非零常数后，事实上只有三个相互独立的常数。所以理论上，我们在求所需要的分式线性映射时，最多只需要找到三对点的映射关系就可以唯一确定分式线性映射——详细地来说，我们只需要两个点+任意一对点就可以写出分式线性映射。这两个点为分子的零点和分母的零点，它们被映射到了象平面的零点和无穷远点。而另外一对点被用作调整整个映射的系数。以一个例子来说明这个问题:

[e.g.]将上半圆

映射为第一象限

解决这类保角映射问题的第一步是“找到在象平面和原象平面上相同的角”，这也是保角映射的名称来源。可以看得出来，在

处圆弧和实轴形成了直角交角，这恰好与第一象限在原点处的角相吻合，所以
是分式线性映射分子的零点，
是分母的零点。

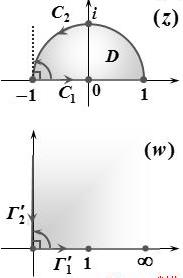
d04b5f92cd678faf578dd522150782be.png

具体来说，它是

。最后所做的即为再找一对特殊点来确定系数
，在图中可以找到的特殊点有
,其中
分别被映射到了实轴和虚轴上。我们令
，不难求出
——在求出
后，

综上，

即为所求映射。
注意：
将半径为
的上半圆映射为第一象限，需要记住。

[e.g.]将圆

映射成右半平面

由于在原图中并没有任何的“角”，所以我们可以直接进入分子分母零点对应的那一步。例如例如

就是可以选择的一对关系。

映射为

。

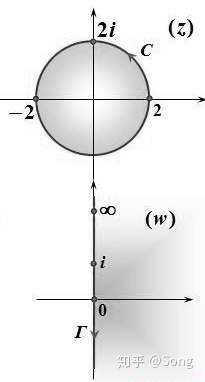
825b07e70147ac968142ad04ec5e559a.png

为了寻找

，我们让

代入后可得，

.

从这个例子我们可以观察边界对应原理和保圆性结合是如何发挥作用的：在沿着

平面的圆弧
的过程中，圆内部的区域始终在绕行方向的左手边。而在
平面的对应点（圆弧和直线的对应是由保圆性决定的）
的过程中，右半平面也始终在行进方向的左手边。这和边界对应原理所指出的区域关系是一致的。

需要注意的是，

在边界对应原理中并不是一个理想的起点，因为只要在距离原点足够远的地方，都可以认为是所在处。这也就是为何在确定一对分子分母零点后无法直接写出分式线性映射的原因——我们还需要一对有限点之间的映射来进行边界对应原理的验证。

上面两个例子都是给定象和原象来找到分式线性映射的形式的，在实际的题目中还可能遇到诸如“寻找上半圆

在
下的象”这样的问题。其解决方法是类似的：找到原象中“角”所在的点，在图中标出分式线性映射的零点和极点，利用保圆性描出完整的象边界，最后用边界对应原理验证沿象区域边界行进时区域内侧的位置是否正确。

在大致了解了分式线性映射后，我们还要研究我们已经了解过的函数在保角映射的观点下具有怎样的几何意义。

（1）（整数）幂函数

根据我们已经了解的知识，幂函数是一个在

平面上处处可导的函数（并且除了0点之外，所有的点导数均不为0）。但它在整个
平面上不是双方单值的。

例如，对

，可以得知

只有对

内的点，幂函数
才是保角映射。

在几何上，它指的是把

为顶点的角形区域映射成
为顶点的角形区域，且张角扩大为原来的
倍。

它的反函数

把角形域映射成角形域，但张角缩小到原来的
倍。

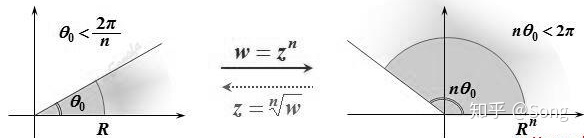
a933b684fc6c08fb8b4d3e3a61e8f14b.png
*需要注意的是，如果角形区域为扇形，则一定要注意扇形的半径是否发生了变化。

（2）指数函数

根据复指数函数的定义，可以知道

也就是

.

这个式子意味着：

的实部可以得到
的模，
的虚部可以得到
的幅角

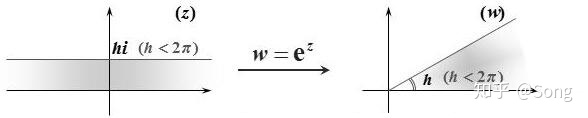
b6bbd18e025cfbe33a30564b39e3ff1e.png

它的映射作用是将高度

的水平带形（也可以是有限/半无穷的矩形）区域变为角形域。

特别地，高度为

的矩形区域会被映射成为上半圆。

它的反函数是

，也即
的第一个主值分支。

在我们研究了（整数）幂函数和指数函数后，我们很自然地可以提出这样一个问题：在下图从

到
平面的映射过程中，标上（？）的映射路径是否是可行的？

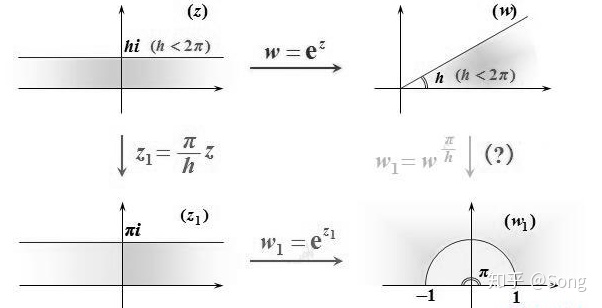
4a56f233c2cfafd5c7fb5452a6ce518f.png

答案是否定的。事实上，在标（？）的路径中，我们使用到了非整数幂的幂函数。对于幂函数而言，

是单值函数，而非整数指数幂
中的
会产生多值性，从而它不是一个良好的能够将
平面的点一一映射到
平面的方式。在运用幂函数进行处理时，一定要关注两点：幂函数是否是整数指数幂的；映射区域是否在
内。

一个常见的映射思路如下：

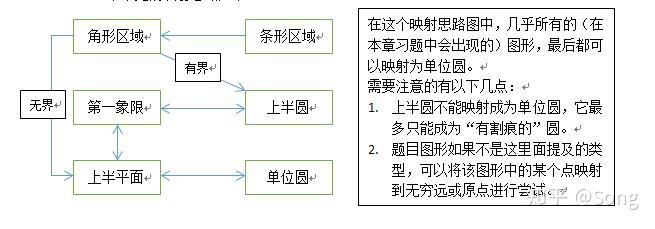
9b5085a1daa727795b4699c482a090ce.png

结语：复变函数的专栏到此就结束了。至于积分变换，我还在结合信号处理等通信类课程一起写作。这会是一个较为复杂和漫长的过程，所以敬请期待。

更多相关：

  • Mapping Persistence Classes 笔记2---ValueType的形式和映射

    2010年5月17日 简介： 前面的笔记着重讲解了实体类以及其class-mapping options，本章笔记将关注值类型的形式以及其OR映射选项。 值类型一般可分为两类：JDK类型和用户自定义类型。本章首先从实体类的使用JDK类型的properties开始，讲解基本的映射元素和映射属性；然后关注自定义的value-type的c...

  • CreateFileMapping

    CreateFileMapping 　　VB声明 　　Declare Function CreateFileMapping Lib "kernel32" Alias "CreateFileMappingA" (ByVal hFile As Long, lpFileMappigAttributes As SECURITY_ATT...

  • 抖音的标题写什么内容_看了这篇文章，我才真正明白什么才是英语速成之路！感恩...

    英语的重要性，毋庸置疑！尤其对广大职场人士，掌握英语意味着就多了一项竞争的技能。那，对于我们成人来说，时间是最宝贵的。如何短时间内在英语方面有所突破，这是我们最关心的事情。英语学习，到底有没有捷径可以走，是否可以速成？周老师在这里明确告诉大家，英语学习，没有绝对的捷径走，但是可以少走弯路。十多年的教学经验告诉我们，成功的学习方法可以借...

  • python显示行数_在idle中如何显示行号

    展开全部 其实IDLE提供了一个显32313133353236313431303231363533e78988e69d8331333365663438示所有行和所有字符的功能。 我们打开IDLE shell或者IDLE编辑器，可以看到左下角有个Ln和Col，事实上，Ln是当前光标所在行，Col是当前光标所在列。 我们如果想得到文件代码...

  • class没有发布到tomcat_Tomcat 在 SpringBoot 中是如何启动的

    前言[1]从 Main 方法说起[2]走进 Tomcat 内部[3]总结[4]《Java 2019 超神之路》《Dubbo 实现原理与源码解析 —— 精品合集》《Spring 实现原理与源码解析 —— 精品合集》《MyBatis 实现原理与源码解析 —— 精品合集》《Spring MVC 实现原理与源码解析 —— 精品合集》《Spri...

  • 如何学习streamdecoder类_如何学习篇5：强化2种能力——2种学习模式之运动类：隐性学习...

    【本文摘要】【注】本文所述内容为学习Yjango《学习观》相关视频之后的总结，观点归Yjango所有，本文仅作为学习之用。阅读本节，会让你对英语这类运动类知识的学习豁然开朗，你会知道英语学习方面，我们的症结所在。学习英语这类运动类知识，需要把握四个原则第一，不要用主动意识。第二，关注于端对端第三，输入输出符合实际情况第四，通过多个例子...

  • 结构化场景中的RGB-D SLAM

    点云PCL免费知识星球，点云论文速读。文章：RGB-D SLAM with Structural Regularities作者：Yanyan Li , Raza Yunus , Nikolas Brasch , Nassir Navab and Federico Tombari编译：点云PCL代码：https://github.co...

  • excel高级函数_PowerQuery 进阶之 M 函数学习

    草色新雨中， 松声晚窗里。之前我们学习 Power Query 都是用鼠标就完成了很多复杂的操作。虽然 PowerQuery 已经将大部分常用功能内置成到功能区。基本能完成我们大部分的报表自动化功能。但是总有些复杂的或者个性化的问题是开发团队没有预先想到的，这时我们就需要学习 M 语言。一、M 语言在哪里？M语言的函数公式有三个地...

  • python从0开始学编程课件_小白从零开始学编程(三)--python基本概念

    前言从2020年3月份开始，计划写一系列文档--《小白从零开始学编程》，记录自己从0开始学习的一些东西。第一个系列：python，计划从安装、环境搭建、基本语法、到利用Django和Flask两个当前最热的web框架完成一个小的项目第二个系列：可能会选择Go语言，也可能会选择Vue.js。具体情况待定，拭目以待吧。。。基本概念表达式表...

  • python 函数递归一次增加一次变量_python3--函数(函数，全局变量和局部变量，递归函数)...

    1.1函数1.1.1什么是函数函数就是程序实现模块化的基本单元，一般实现某一功能的集合。函数名：就相当于是程序代码集合的名称参数：就是函数运算时需要参与运算的值被称作为参数函数体：程序的某个功能，进行一系列的逻辑运算return 返回值：函数的返回值能表示函数的运行结果或运行状态。1.1.2函数的作用函数是组织好的，可重复使用的，用来...

  • python深度神经网络量化_基于Python建立深度神经网络！你学会了嘛？

    原标题：基于Python建立深度神经网络！你学会了嘛？图1 神经网络构造的例子(符号说明：上标[l]表示与第l层；上标(i)表示第i个例子；下标i表示矢量第i项)单层神经网络图2 单层神经网络示例神经元模型是先计算一个线性函数(z=Wx+b)，接着再计算一个激活函数。一般来说，神经元模型的输出值是a=g(Wx+b)，其中g是激活函数(...

  • mysql 字段加减_MySQL中你必须了解的函数

    在学习MySQL的时候你会发现，它有非常多的函数，在学习的时候没有侧重。小编刚开始学习的时候也会有这个感觉。不过，经过一段时间的学习之后，小编发现尽管函数有很多，但是常用的却只有那几个。今天小编就把常用的函数汇总一下，为大家能够能好的学习MySQL中的函数。MySQL常使用的函数大概有四类。时间函数、数学函数、字符函数、控制函数。让我...

©2024 11GX.COM