jquery判断方法是否存在_判断图中是否有环的三种方法
0、什么是环?
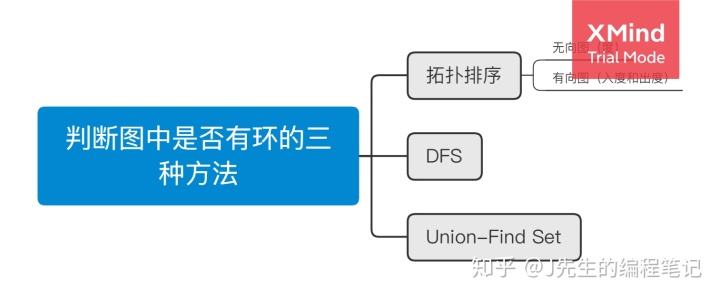
在图论中,环(英语:cycle)是一条只有第一个和最后一个顶点重复的非空路径。
在有向图中,一个结点经过两种路线到达另一个结点,未必形成环。
1、拓扑排序
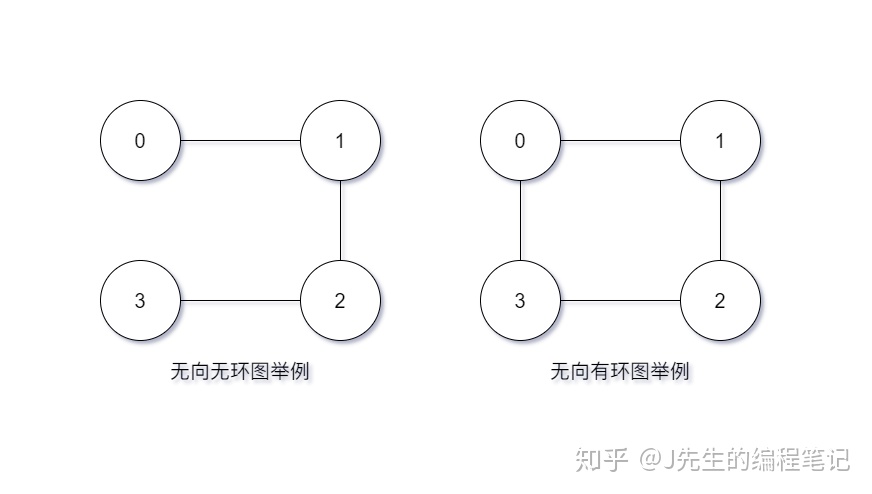
1.1、无向图
使用拓扑排序可以判断一个无向图中是否存在环,具体步骤如下:
- 求出图中所有结点的度。
- 将所有度 <= 1 的结点入队。(独立结点的度为 0)
- 当队列不空时,弹出队首元素,把与队首元素相邻节点的度减一。如果相邻节点的度变为一,则将相邻结点入队。
- 循环结束时判断已经访问的结点数是否等于 n。等于 n 说明全部结点都被访问过,无环;反之,则有环。
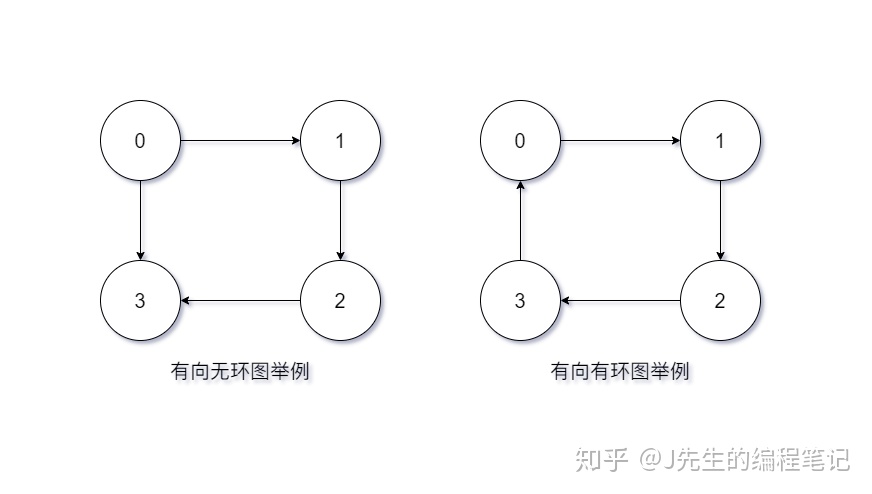
1.2、有向图
使用拓扑排序判断无向图和有向图中是否存在环的区别在于:
- 在判断无向图中是否存在环时,是将所有**度 <= 1** 的结点入队;
- 在判断有向图中是否存在环时,是将所有**入度 = 0** 的结点入队。(感谢 wangweijun@shen 指正!!!)
2、DFS
使用 DFS 可以判断一个无向图和有向中是否存在环。深度优先遍历图,如果在遍历的过程中,发现某个结点有一条边指向已访问过的结点,并且这个已访问过的结点不是上一步访问的结点,则表示存在环。
我们不能仅仅使用一个 bool 数组来表示结点是否访问过。规定每个结点都拥有三种状态,白、灰、黑。开始时所有结点都是白色,当访问过某个结点后,该结点变为灰色,当该结点的所有邻接点都访问完,该节点变为黑色。
那么我们的算法可以表示为:如果在遍历的过程中,发现某个结点有一条边指向灰色节点,并且这个灰色结点不是上一步访问的结点,那么存在环。

#include 3、Union-Find Set
我们可以使用并查集来判断一个图中是否存在环:
对于无向图来说,在遍历边(u-v)时,如果结点 u 和结点 v 的“父亲”相同,那么结点 u 和结点 v 在同一个环中。
对于有向图来说,在遍历边(u->v)时,如果结点 u 的“父亲”是结点 v,那么结点 u 和结点 v 在同一个环中。
#include References
- 环 (图论)
- 有向无环图
- 判断一个图是否有环及相关 LeetCode 题目
- 判断有向图是否存在环的 2 种方法(深度遍历,拓扑排序)
更多相关:
-
已知一个长度为11的线性表List=(12, 24, 36, 90, 52, 30, 41, 8, 10, 38, 61),试回答下面问题 (1)将线性表元素依次插入一个空的平衡二叉树,画出所得平衡二叉树,如果假设每个元素查找概率相同,则平均查找长度为多少? (1) 插入12, 这是第一个结点,是根结点. (2) 插入...
-
对该问题,分为如下几种情形讨论: 情形一: 假如该树为二叉树,并且是二叉搜索树, 依据二叉搜索树是排过序的, 我们只需要从树的根结点开始,逐级往下,和两个输入的结点进行比较. 如果当前结点的值比两个结点的值都大,那么最低的公共祖先一定在当前结点的左子树中,下一步遍历当前结点的左子节点. 如果当前结点的值比两个结点的值都小,那么...
-
哗我看了一下好像没有很详细专门讲分治的blog?那就主要先学一下点分治吧,其他的……等我记得把C++一本通带到机房来再说吧先咕着啦 写在前面 刷题进度 入门题(0/3) 好题(0/9) 问题解决进度 Q1 Q2 正文 淀粉质 点分治 点分治就是在一棵树上,对具有某些限定条件的途径静态地进行统计的算法。 ——《算法竞赛 进阶指南》...
-
B树 即二叉搜索树: 1.所有非叶子结点至多拥有两个儿子(Left和Right); 2.所有结点存储一个关键字; 3.非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树; 如: ...
-
1、百分号无限循环小数 2、小数四舍五入计算错误 3、写死了年份导致跨年无法选择最新年份 4、悄悄修改内外网访问限制导致外网接口不能访问 5、定位索引城市的地理坐标,定位到了同名的其他城市 6、更新包的时候没传完就关电脑 7、前后端绑定字段不统一,字段类型不统一 【对接】《前后端对接联调数据、调试接口过程乌龙大合集》_←...
-
我和你不了的故事——代腾飞 2006年12月11日 于成都你无言告别而消失得无影无踪我的世界只留下了你昔日的背影从此你我相隔在不远不近的时空里然而我却失去了你所有的联系你带走的是我们在一起的欢歌笑语为我留下的却是思念的苦楚和美妙而难忘的回忆不知此时的你是否偶尔能把我记忆不知在你梦里我们是否还能相会午夜醒来的时候是否还会把我想起我和...