有一个1亿结点的树,已知两个结点, 求它们的最低公共祖先!

首页 > 有一个1亿结点的树,已知两个结点, 求它们的最低公共祖先!

有一个1亿结点的树,已知两个结点, 求它们的最低公共祖先!

对该问题,分为如下几种情形讨论:

情形一:

假如该树为二叉树,并且是二叉搜索树, 依据二叉搜索树是排过序的, 我们只需要从树的根结点开始,逐级往下,和两个输入的结点进行比较.

如果当前结点的值比两个结点的值都大,那么最低的公共祖先一定在当前结点的左子树中,下一步遍历当前结点的左子节点.

如果当前结点的值比两个结点的值都小,那么最低的公共祖先一定在当前结点的右子树中,下一步遍历当前结点的右子结点.

这样在树中从上到下找到的第一个在两个输入结点的值之间的结点,就是最低的公共祖先.

情形二:

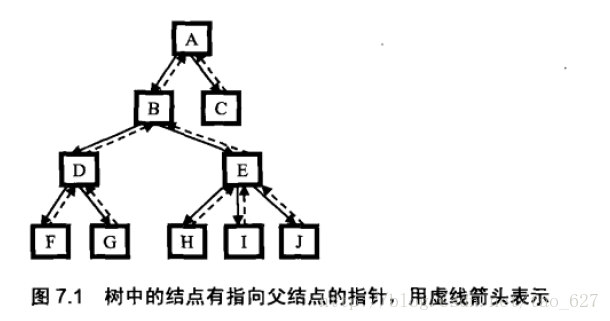
如果是一棵普通的树,但是树的结点(除根结点外)中有指向父结点的指针:

这个问题可以转换为求两个链表的第一个公共结点.

假设树结点中指向父结点的指针是pParent,那么从树的每一个叶结点开始都一个由指针pParent串起来的链表,这些链表的尾指针都是树的根结点.

输入两个结点,这两个结点位于两个链表上,它们的最低公共祖先刚好是这两个链表的第一个公共结点. 比如输入的两个结点分别为F和H,那么F在链表F->D->B->A上,

而H在链表H->E->B->A上, 这两个链表的第一个交点B 刚好也是它们的最低公共祖先.参见下面的图示

情形三:

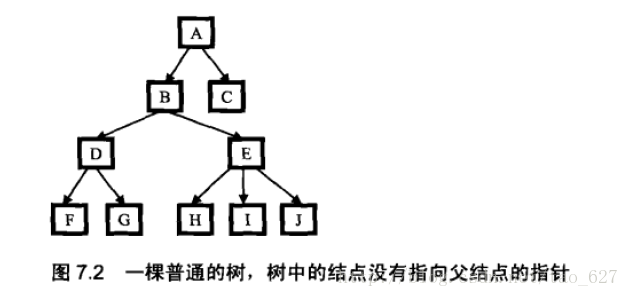
仅是一棵普通的树,没有其它条件:

求出从根结点到指定结点的路径,这样我们就得到两条路径,比较这两条路径的最低公共祖先就可以了.

具体的思路还是,从树的根节点开始遍历,参见下面的图,

假设还是输入结点F和H, 我们先判断A的子树中是否同时包含结点F和H, 得到的结果为true,接着我们再先后判断A的两个子结点B和C的子树是否同时包含F和H,结果是B的结果为true而C的结果是false, 接下来我们再判断B的两个子结点D和E,发现这两个结点得到的结果都是false,于是B是最后一个公共祖先,即是我们的输出.

这里需要注意的问题是, 如何避免对同一个结点重复遍历很多次的问题?

比如当我们判断以结点A为根的树中是否含有结点F的时候, 我们需要对D,E等结点遍历一遍；接下来判断以结点B为根的树中是否含有结点F时, 我们还是需要对D,E等结点再次遍历一遍.

解决这个问题的思路是:

在遍历的过程中使用辅助缓存,用两个链表分别保存从根结点到输入的两个结点之间的路径,然后把问题转换为两个链表的最后公共结点的问题.

比如我们用前序遍历的方法得到从根结点A到H的路径的过程如下:

(1)遍历到A,将A放入路径中,路径中只有一个结点A;

(2)遍历到B,把B存到路径中去,此时路径为A->B;

(3)遍历到D,把D放到路径中去,此时路径为A->B->D;

(4)遍历到F,把F放到路径中去,此时路径为A->B->D->F;

(5)F为叶结点,这条路径不可能到达节点H,我们需要回溯,把F从路径中删除,变为A->B->D;

(6)遍历到G,和结点F一样,这条路径无法到达H,遍历玩G后,这条路径仍是A->B->D;

(7)由于D的所有结点都遍历过了,不可能到达结点H, 因此D不在路径中,将D从路径中删除,变成A->B;

(8)遍历E,把E加入到路径中,此时路径变成A->B->E;

(9)遍历H,已经到达目标结点,A->B->E就是根结点开始到达H必须经过的路径.

按照上面的方法,我们同理可以得到从根结点A开始到F必须经过的路径是A->B->D.

接着,我们求出这两个路径的最后公共结点,也就是B,就是我们要求的F和H的最低公共祖先.

时间复杂度分析:

为了得到从根结点开始到输入的两个结点的两条路径,需要遍历两次树,每次遍历的时间复杂度是O(n),得到的两条路径的长度在最差的情况是O(n),通常情况下两条路径的长度是O(logn)

下面是情形三的实现代码,文件名为common_parent_in_tree.cpp

#include "tree.h"
#include using namespace std;bool GetNodePath(TreeNode* pRoot, TreeNode* pNode, list& path){if(pRoot == pNode)return true;path.push_back(pRoot);bool found = false;vector::iterator i = pRoot->vec_children.begin();while(!found && ivec_children.end()){found = GetNodePath(*i, pNode, path);++i;}if(!found)path.pop_back();return found;
}TreeNode* GetLastCommonNode(const list& path1, const list& path2){list::const_iterator iterator1 = path1.begin();list::const_iterator iterator2 = path2.begin();TreeNode* pLast = NULL;while(iterator1 != path1.end() && iterator2 != path2.end()){if(*iterator1 == *iterator2)pLast = *iterator1;iterator1++;iterator2++;}return pLast;
}TreeNode* GetLastCommonParent(TreeNode* pRoot, TreeNode* pNode1, TreeNode* pNode2){if(pRoot == NULL || pNode1 == NULL || pNode2 == NULL)return NULL;list path1;GetNodePath(pRoot, pNode1, path1);list path2;GetNodePath(pRoot, pNode2, path2);return GetLastCommonNode(path1,path2);
}//===========================测试代码==================================void Test(const char* testName, TreeNode* pRoot, TreeNode* pNode1, TreeNode* pNode2, TreeNode* pExpected){if(testName != NULL)printf("%s begins: 
", testName);TreeNode* pResult = GetLastCommonParent(pRoot, pNode1, pNode2);if((pExpected == NULL && pResult == NULL) ||(pExpected != NULL && pResult != NULL && pResult->value == pExpected->value))printf("Passed.
");elseprintf("Failed.
");
}// 形状普通的树
//                     1
//                    / 
//                   2   3
//                  / 
//                 4   5
//                /  /|
//               6  78 9 10
void Test1(){TreeNode* pNode1 = CreateTreeNode(1);TreeNode* pNode2 = CreateTreeNode(2);TreeNode* pNode3 = CreateTreeNode(3);TreeNode* pNode4 = CreateTreeNode(4);TreeNode* pNode5 = CreateTreeNode(5);TreeNode* pNode6 = CreateTreeNode(6);TreeNode* pNode7 = CreateTreeNode(7);TreeNode* pNode8 = CreateTreeNode(8);TreeNode* pNode9 = CreateTreeNode(9);TreeNode* pNode10 = CreateTreeNode(10);ConnectTreeNodes(pNode1,pNode2);ConnectTreeNodes(pNode1,pNode3);ConnectTreeNodes(pNode2,pNode4);ConnectTreeNodes(pNode2,pNode5);ConnectTreeNodes(pNode4,pNode6);ConnectTreeNodes(pNode4,pNode7);ConnectTreeNodes(pNode5,pNode8);ConnectTreeNodes(pNode5,pNode9);ConnectTreeNodes(pNode5,pNode10);Test("Test1", pNode1, pNode6, pNode8, pNode2);
}//树退化为一个链表
//                    1
//                   /
//                  2
//                 /
//                3
//               /
//              4
//             /
//            5
void Test2(){TreeNode* pNode1 = CreateTreeNode(1);TreeNode* pNode2 = CreateTreeNode(2);TreeNode* pNode3 = CreateTreeNode(3);TreeNode* pNode4 = CreateTreeNode(4);TreeNode* pNode5 = CreateTreeNode(5);ConnectTreeNodes(pNode1,pNode2);ConnectTreeNodes(pNode2,pNode3);ConnectTreeNodes(pNode3,pNode4);ConnectTreeNodes(pNode4,pNode5);Test("Test2",pNode1,pNode5,pNode4,pNode3);
}//树退化为一个链表,一个结点不在树中
//                    1
//                   /
//                  2
//                 /
//                3
//               /
//              4
//             /
//            5         6
void Test3(){TreeNode* pNode1 = CreateTreeNode(1);TreeNode* pNode2 = CreateTreeNode(2);TreeNode* pNode3 = CreateTreeNode(3);TreeNode* pNode4 = CreateTreeNode(4);TreeNode* pNode5 = CreateTreeNode(5);ConnectTreeNodes(pNode1,pNode2);ConnectTreeNodes(pNode2,pNode3);ConnectTreeNodes(pNode3,pNode4);ConnectTreeNodes(pNode4,pNode5);TreeNode* pNode6 = CreateTreeNode(6);Test("Test3",pNode1,pNode5,pNode6,NULL);
}//输入NULL
void Test4(){Test("Test4", NULL, NULL, NULL, NULL);
}int main(int argc, char** argv){Test1();Test2();Test3();Test4();return 0;
}

下面是程序运行结果的截图:

有一个1亿结点的树,已知两个结点, 求它们的最低公共祖先!

更多相关：

jquery判断方法是否存在_判断图中是否有环的三种方法

简单的平衡二叉树

（点）分治学习笔记

B树，B+树，B-树和B*树

剑指offer：面试题32 - II. 从上到下打印二叉树 II

剑指offer：面试题28. 对称的二叉树

剑指offer：面试题27. 二叉树的镜像

剑指offer：面试题26. 树的子结构

tree类型题目需要用到的头文件tree.h

python绝对路径的区别_python学习：绝对路径和相对路径

c++ 工作路径介绍及获取

修改IDEA运行jsp文件的时候浏览器地址栏的虚拟访问路径网址

vue引入图片路径的三种主要方法

地图收敛心得170405