C# 篇基础知识11——泛型和集合

.NET提供了一级功能强大的集合类，实现了多种不同类型的集合，可以根据实际用途选择恰当的集合类型。

除了数组 Array 类定义在System 命名空间中外，其他的集合类都定义在System.Collections 命名空间中。为了方便、快捷地操纵集合元素，.NET 专门为集合定义了一套接口，.NET 中的集合类都实现了一个或多个接口，并且每个集合类都拥有适合自身特点的独有方法，因此可以非常方便的操控集合中的元素。

为何对于集合类元素，可以使用foreach方法进行遍历，这是因所有的集合都直接或间接地实现了IEnumerable接口，这个接口定义了GetIEnumerator()方法，该方法返回了一个IEnumerator对象称为为迭代器，foreach语句就是通过访问迭代器而获取集合中元素的。

public interface IEnumerator

{  bool MoveNext();  //获取下一个元素

   object Current{get;}  //获取当前元素

   void Reset();  //将枚举数设置为其初始位置   }

ICollection接口也是一个很基础的接口，它继承于IEnumerable，并且添加了一个CopyTo()方法，一个Count属性以及两个用于同步的属性。

public interface ICollection : IEnumerable

{ void CopyTo(System.Array array, int index); //复制到数组

int Count { get; } //元素个数

bool IsSynchronized { get; } //是否同步

object SyncRoot { get; } //用于同步的对象  }

IList 接口和IDictionary 接口都继承于ICollection 接口。

Array类，C#为创建数组提供了专门的语法。数组有一个非常显著的优点，即可以根据下标高效地访问数组的元素；但是数组也有一个缺点，即在创建时数组的大小就已经确定了，不能动态地增加元素。Array 类有许多有用的方法，例如静态方法Sort()方法和Copy()方法，Sort()方法的功能是对数组排序，Copy()方法的功能是复制数组，它有三个参数，第一个参数是原数组，第二个参数是目标数组，第三个参数表示复制元素的个数。

1.泛型

泛型是C#2.0 推出的一个新特性，通过它可以定义像文档模板一样的类模板。

（1）泛型的概念

在 ArrayList、Stack、Queue 等集合类中，元素的类型均为Object。由于.NET 中所有类都继承于Object，所以这些集合可以存储任何类型的元素。使用这些集合添加元素和读取元素时分别需要装箱和拆箱操作，例如：

ArrayList list = new ArrayList();

list.Add(10); //添加元素

int n = (int)list[0];

这样做有三个缺点：

第一，在装箱、拆箱的过程中，可能会造成一定的性能损失。

第二，无论什么样的数据都能往集合里放，不利于编译器进行严格的类型安全检查。

第三，显式转换会降低程序的可读性。

为解决这些问题，C#2.0推出了泛型（Generic），泛型集合类和非泛型集合类功能上基本一致，唯一的区别是泛型集合类的元素类型不是Object，而是自己指定的类型。

例如可以自行定义一个队列泛型类public class MyQueue｛｝,，泛型类与普通类的区别是它具有一个类型参数列表，在整个类里用T 代表元素类型。在定义类的时候，元素类型是未知的，是一个抽象的类型。在使用泛型类时，应为抽象类型T 指定具体类型。例如：

//使用时用int 替换抽象类型T

MyQueue q1 = new MyQueue(20);

//用char 替换抽象类型T

MyQueue q2 = new MyQueue(20);

用具体值类型int代替抽象类型T时，公共语言运行时在进行JIT 编译时，会用int 代替泛型类中的T，创造出一个以int 为元素类型的新类，这个过程称为泛型类型的实例化（Generic Type Instantiation）。不同的值类型，会实例化出不同的新类。但对于所有引用类型共享同一个MyQueue实例，因为集合中只会存储对象的引用符，而所有对象的引用符都占用4 个字节。

除了定义泛型类，还可定义泛型方法、泛型接口、泛型结构体、泛型委托等。和泛型类一样，使用泛型方法时也要为把抽象类型具体化。泛型的定义中可含有多个类型参数。例如泛型类class Dictionary{…}。

泛型最常见的用途是定义泛型集合，泛型集合和相对应的非泛型集合功能基本相同，但泛型集合能提供严格的类型检查，具有较强的安全性。此外，如果元素类型为值类型，泛型集合的性能通常优于非泛型集合。泛型集合类定义在System.Collections.Generic 命名空间中。

（2）列表

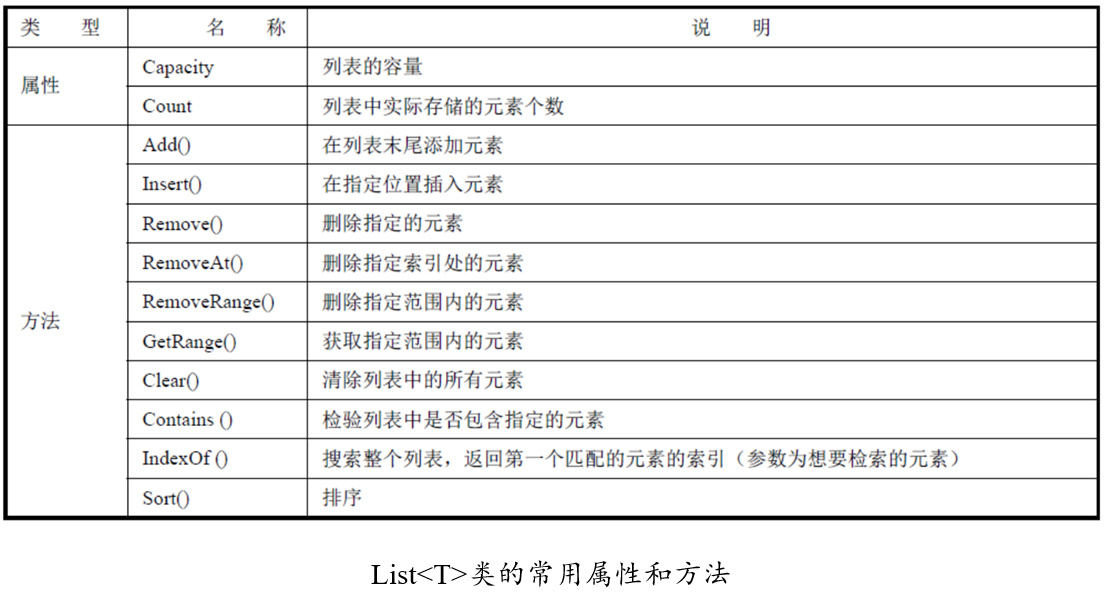
列表在非泛型集合中用 ArrayList 类实现，在泛型集合中用List类实现。列表与数组类非常类似，其区别是数组不能改变大小，而列表可以改变大小。

List basketballPlayers = new List(); //默认容量为0

List basketballPlayers = new List(10); //容量为10

basketballPlayers.Capacity = 10;//改变列表的容量

当列表的容量改变时，系统会分配新的内存空间，创建一个全新的列表，然后把原列表的内容复制到新列表中，最后删除原列表。向已经装满的列表添中加新元素时，列表会采用“翻倍”的办法增加容量。现在basketballPlayers 是一个容量为10 的列表，当添加第11 项时，就会创建一个新的容量为20 的列表。容量翻倍貌似浪费内存空间，但这是一个使列表“合适增长”的高效方法。如果每次添加一个新元素就重新创建一次列表，其效率低下可想而知。访问列表元素的方式和数组一样，都是通过索引来访问。例如：string name = basketballPlayers[2]; 。List类的部分重要方法：

Add()方法，Add()方法用于向列表中添加元素，新元素位于列表的末尾，例如basketballPlayers.Add("姚明");。

Remove()方法，Remove()方法用于删除元素，参数为欲删除的对象。如果删除成功，返回true；如果删除不成功或欲删除的对象不存在，返回false，例如basketballPlayers.Remove("邓肯");。

RemoveAt()方法，使用Remove()方法时，系统需要在列表中进行搜索，以便找到匹配的元素，这个搜索过程需要花费一定的时间。RemoveAt()方法的参数为元素的索引，可以直接删除指定位置上的元素。例如basketballPlayers.RemoveAt(2);。

Insert()方法，Insert()方法用于在指定位置插入元素。basketballPlayers.Insert(2, "诺维斯基");

RemoveRange()方法，RemoveRang()方法可以一次从列表中删除多个元素，它的第一个参数表示起始位置，第二个参数表示从该位置起删除几个元素。例如basketballPlayers.RemoveRange(1, 3);。

AddRange()方法，AddRange()方法用于一次性添加一批元素，它的参数是一个集合，集合中包含所有要添加的元素。例如：string[] names ={ "邓肯", "阿伦", "加索尔" }; basketballPlayers.AddRange(names);。

GetRange()方法，GetRange()方法用于获取列表中指定范围内的元素，它的第一个参数表示起始位置，第二个参数表示从该位置起读取几个元素。List bestPlayers = basketballPlayers.GetRange(0,3);。

（3）栈

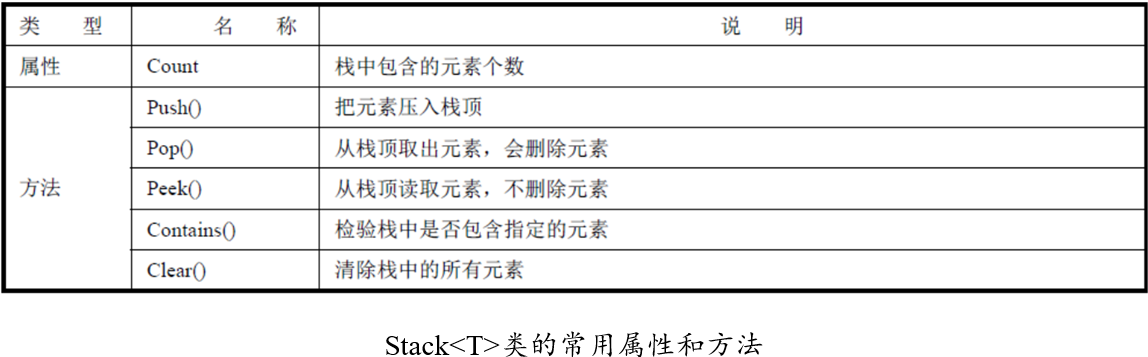
栈是一种后进先出（Last In First Out，LIFO）的集合类型，栈在非泛型集合中用Stack类实现，在泛型集合中用Stack类实现，下面介绍一下泛型类Stack中的重要属性和方法。

Push()方法，在栈顶添加元素的操作称为压栈，用Push()方法实现，例如Stack alphabet = new Stack(); alphabet.Push('A');。

Pop()方法，从栈顶取出元素的方法称为出栈，用 Pop()方法实现，例如char leter = alphabet.Pop();。使用Pop()方法后元素将从栈中删除。

Peek()方法，用来读取栈顶的元素，但不删除它。

（4）队列

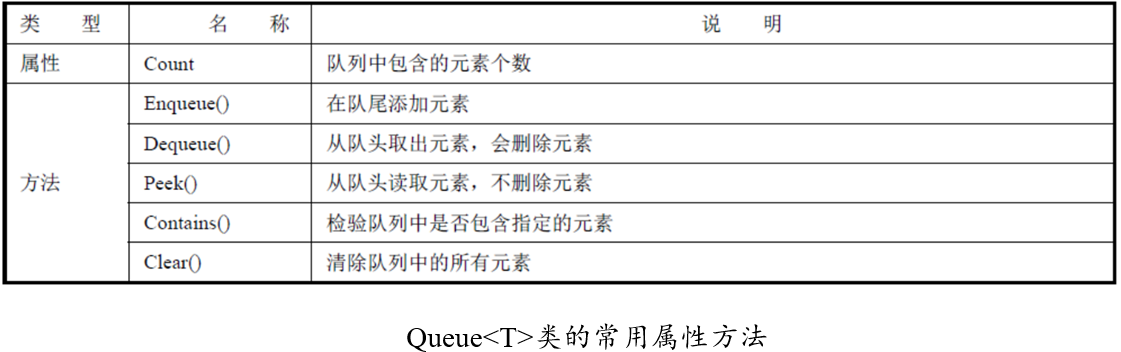
队列（Queue），队列的元素只能从队头取出，从队尾加入，是一种先进先出（First In First Out，FIFO）的集合类型。队列在非泛型集合中用 Queue 类实现，在泛型集合中用Queue 类实现，下面介绍一下泛型类Queue 中的重要属性和方法。

Enqueue()方法，在队尾添加元素称为入队，用 Enqueue()方法实现。例如

Queue alphabet = new Queue();

alphabet.Enqueue('A');

alphabet.Enqueue('B');

遍历时，也将按入队的顺序显示。

Dequeue()方法，从队头取出元素称为出队，用Dequeue()方法实现，取出的元素会被删除。

Peek()方法，Queue 类也有Peek()方法，它用来读取队头的元素，但不删除元素。

 

（5）排序列表

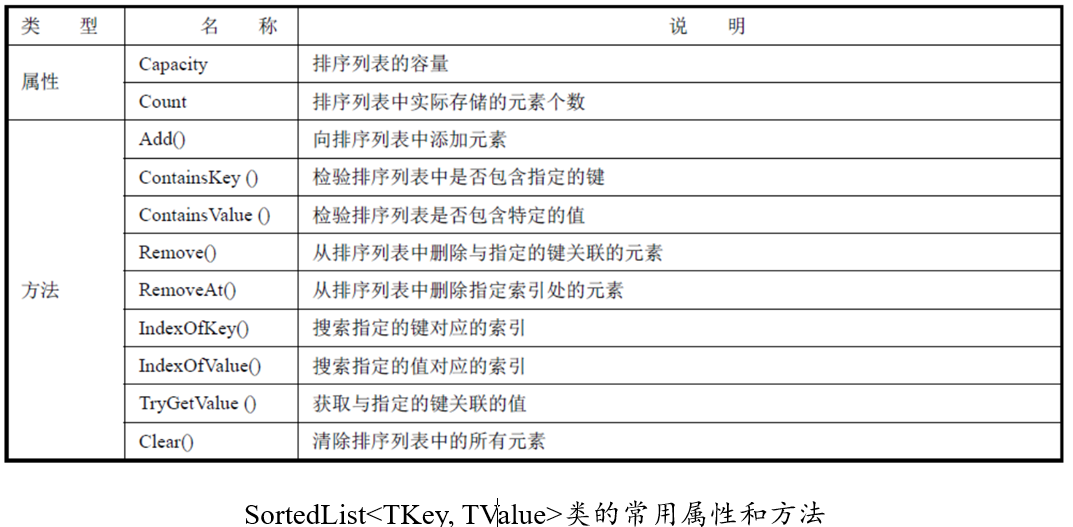
排序列表与列表很相似，区别是排序列表中的每个元素都与一个用于排序的键（Key）关联，元素按键的顺序排列。实际上排序列表内部维护两个数组，一个数组用于存储元素，另一个数组用于存储与元素关联的键。排序列表在非泛型集合中用 SortedList 类实现，在泛型集合中用SortedList类实现，下面介绍一下泛型类SortedList中的重要属性和方法。

通过 SortedList类的Add()方法可以向集合中添加元素，它有两个参数，第一个参数是与元素关联的键，第二个参数是元素的值。例如：

SortedList medalTable = new SortedList(); medalTable.Add(3, "吴敏霞");

medalTable.Add(1, "郭晶晶");

medalTable.Add(2, "哈莉娜");

//输出结果

for (int i = 0; i < medalTable.Count; i++)

{Console.WriteLine(medalTable.Keys[i] + " : " + medalTable.Values[i]);}

SortedList类的Count 属性为列表中实际存储的元素个数，Keys 属性为所有键的集合，Values 属性为所有值的集合。上述程序输出结果为：1：郭晶晶 2：哈莉莉 3：吴敏霞。可以发现，排序列表中的元素并不是按添加顺序排列的，而是按照键的顺序排列的。

（6）散列表

散列表（Hashtable）又叫做字典（Dictionary），能够非常快速的添加、删除和查找元素，是现在检索速度最快的数据结构之一。

散列函数能根据Key 直接计算出元素的索引，能否设计一个有效的散列函数，是解决问题的关键，然而现实世界并非总是那么完美，实际数据也并不总是那么配合散列函数，会出现各种各样的问题。一种问题是元素的散列码不连续，这种问题很好解决，大不了让不连续的地方空在那里即可，虽然有点浪费空间，但因为散列表的读写速度很快，我们“以空间换取了时间”。另一种问题是多个Key具有相同的散列码。。.NET采用了一种精心设计的方法解决冲突①，其基本思想是先通过散列函数计算出基位置，如果发现基位置已经被占用，就根据一定的算法向下寻找，直到找到空位置为止。当然，与之对应，检索元素时也要采取相同的方法。。在实际问题中，散列函数有很多种，我们需要根据Key 的类型和整个集合的特征设计恰当的散列函数。一个设计良好的散列表，应当能使元素均匀分布。

这里讲了散列表的基本原理，实际问题要复杂得多，但基本思想就是一条：用散列函数把元素映射到相应的位置。散列表中的元素可以是基本类型数据，也可以是非常复杂的包含很多成员变量的对象，这时我们需要挑选一个合适的成员变量做键（Key），而整个元素则被称为值（Value）。，.NET 中所有的类都有一个从Object 类继承来的GetHashCode()方法，散列表就是根据这个散列函数计算散列码的。任何类型都可以用作Key，如果你用.NET中预定义的类做Key，散列表就通过该类的GetHashCode()方法计算散列码；如果你想用自己定义的类做Key，一般需要重写GetHashCode()方法。除此之外，散列表还允许我们根据需要指定散列函数，这时不管你的Key 为何种类型，都使用你所指定的散列函数进行计算。

散列表在非泛型集合类中用Hashtable 类实现，在泛型集合类中用Dictionary类实现，下面我们介绍泛型类Dictionary的重要属性和方法。

①构造函数

Dictionary类为我们重载了7 个构造函数，使用该泛型类时需要指明键类型和值类型。

Dictionary colorTable1 = new Dictionary();

除此之外，我们还可为字典提供自定义的GetHashCode()方法。

Dictionary colorTable1 = new Dictionary(comparer);

其中参数comparer 是一个实现了IEqualityComparer 接口的对象，IEqualityComparer 接口定义了两个方法，Equals()方法用来判断两个对象是否相等，GetHashCode()方法用来为字典提供散列函数，这时不管字典中的Key 为何种类型，都将通过comparer 对象提供的散列函数进行散列。为了使字典能够正常工作，编写GetHashCode()方法有相当严格的要求。

②Add()方法

通过 Add()方法向字典中添加元素，它接受两个参数，第一个参数是与元素关联的键（Key），第二个参数是元素的值（Value），字典将根据Key 计算出元素的存储位置。例如：

//创建元素

Color red = new Color("Red", 255, 0, 0);

Color green = new Color("Green", 0, 255, 0);

Color orange = new Color("Orange", 255, 200, 0);

//建立字典

Dictionary colorTable = new Dictionary();

//向字典中添加元素

colorTable.Add(red.Name, red);

colorTable.Add(green.Name, green);

colorTable.Add(orange.Name, orange);

先创建了一个字典，然后向字典中添加了三个Color 对象。这里选取Color 对象的Name 属性作为Key，通过它计算元素在字典中的位置。

③以Key为索引设置或读取元素

colorTable["Blue"] = new Color("Blue", 0, 0, 255); //设置元素：

Console.WriteLine("新添加的元素为: " + colorTable["Blue"]);//输出元素

以这种方法向字典中添加元素与用 Add()方法有一点区别：当字典中已存在该Key 时，Add()方法会引发异常，而以Key 为索引则不会，只是用新值替换旧值而已。

④Keys属性

通过字典的 Keys 属性可以获取字典的所有键。例如foreach (string key in colorTable.Keys){}

⑤Values属性

通过字典的Values属性可以获取字典的所有元素的值，例如：

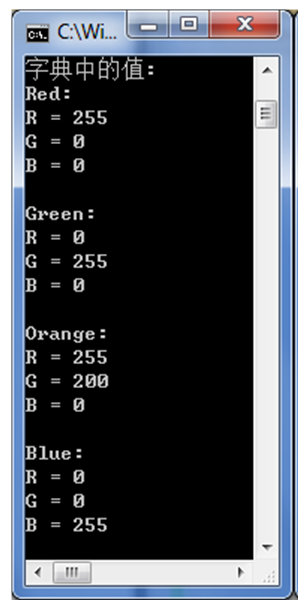
Console.WriteLine("字典中的值:");

foreach (Color value in colorTable.Values)

{Console.WriteLine(value);}

其结果如下图所示。

 

⑥ContainsKey()方法，ContainsKey()方法用于检验字典中是否包含特定的键。因为参数提供了键的信息，所以可通过散列函数找到元素的位置，只需计算一次，效率很高。例如：if (colorTable.ContainsKey("Red")){…}

⑦ContainsValue()方法，用于检验字典中是否包含特定的Value。由于没有键的信息，该方法需要检索整个字典的来寻找元素，平均需要检索n/2 次。例如if(colorTable.ContainsValue(black)){}

⑧Remove()方法，通过字典的 Remove()方法可以删除与指定的键关联的元素。例如：colorTable.Remove("Orange");

综上所述，字典是一种检索速度非常快的数据结构，在拥有海量数据的问题中往往能发挥非常重要的作用。

2.类型约束

在泛型中，类型参数T 可以实例化为任何数据类型，这在某种情况下会产生问题。

//T 代表某种动物类

class AnimalFamily

{//用来存储动物的家庭成员

private List family = new List();

//方法：添加成员

public void Add(T member)

{family.Add(member);}

//方法：显示所有成员

public void Display()

{  foreach (T member in family)

{Console.WriteLine(member.name);}

}

}

主述程序会出现以下编译错误，这是因为member 的类型为T，而T 为何种具体类型并不确定，因此就不能确定member 是否拥有成员变量name。

 

解决办法是对抽象类型 T 进行约束（Constraint），限制T 的取值范围。例如将代码改成如下，在泛型类AnimalFamily中，我们通过where 关键字把类型T 的范围限制在Animal类和它的派生类中，这样就确保对象member 中一定包含成员name，编译也能顺利通过了。

class Animal

{//公有变量

public string name;

//构造函数

public Animal(string nameValue)

{name = nameValue;} }

//泛型类

class AnimalFamily where T : Animal

{…}