在RPG游戏中我们经常会看到一些迷宫,我之前玩仙剑一的时候就经常在几个迷宫里绕来绕去也绕不出来,玩仙三由于游戏视角可以转,更是费劲。这里我们使用深度优先算法达到遍历一个迷宫的目的。
首先定义一个有序元组A:{左,上,右,下}表示遍历的顺序,这个顺序将用来生成搜索树的子节点,当然顺序是可以变的,如果地图是45度角的,也可以定义非正方向,总之能表示一个顺序就好。
然后针对每个分叉节点,定义候选方向为B:{x|x∈A ∩x方向有路可走∩ x≠当前方向},算法每次得到按照A排序的B集合,然后从B中取第一个方向进行,一直到B=Φ。当B=Φ时回溯到上一个节点,然后得到当前节点的B集,从中选择优先级低于当前方向的方向继续前进.如此可以遍历整个迷宫。
本算法的问题在于迷宫必须是非成环的,像仙剑三到大渡口的迷宫就是有环的,所形成的就不是搜索树而是搜索图,另一个问题是如果完全执行算法最后会停在入口的位置,所以见到出口您就出吧,见好就收。
举一个例子。
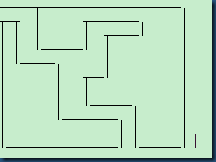
如上图所示的迷宫A集合{左,上,右,下},B集合依次如下所示:
{右}
{下}
{右}
{右,下}选则右
{上}
{右}回退一个
{上}回退一个
{右,下}选择下
{右}
{下}见好就收吧,出迷宫去喽
搜索树如图所示,每个子节点集合就是B
右
|
下
|
右
/
右 下
| |
上 右
| |
右 下
当然实际的迷宫构成的搜索树会很复杂,但是深度优先的思路还是一致的.