首页 > 线段树入门

线段树入门

线段树

 

 

前言

什么是线段树

线段树，是一种二叉搜索树。它将一段区间划分为若干单位区间，每一个节点都储存着一个区间。它功能强大，支持区间求和，区间最大值，区间修改，单点修改等操作。

线段树的思想和分治思想很相像。

线段树的每一个节点都储存着一段区间[L…R]的信息，其中叶子节点L=R。它的大致思想是：将一段大区间平均地划分成2个小区间，每一个小区间都再平均分成2个更小区间……以此类推，直到每一个区间的L等于R（这样这个区间仅包含一个节点的信息，无法被划分）。通过对这些区间进行修改、查询，来实现对大区间的修改、查询。

这样一来，每一次修改、查询的时间复杂度都只为O(logN)，而空间复杂度一般开4N。

但是，可以用线段树维护的问题必须满足区间加法，否则是不可能将大问题划分成子问题来解决的。

 证明：空间复杂度开4N

假设：N=2h   

 

 

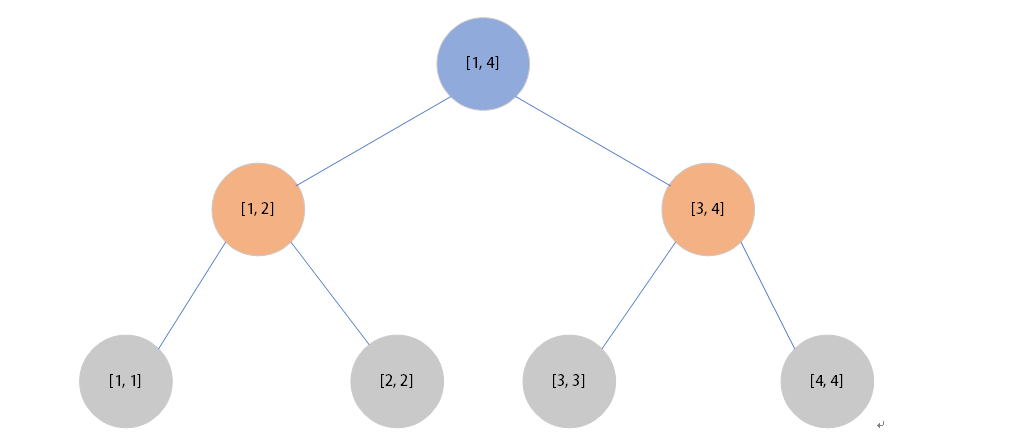
那么layer[0] = 20，layer[1] = 21+……+layer[h] = 2h

Sum = 20+21+22+……+2h  =  = 2*2h-1 = 2N-1

但是这只是特殊情况，大多数情况 N = 2h+M （M<2h）

所有：2h < N < 2h+1     那么    2*2h-1 < Sum < 2*2h+1-1

那我们就取大的，开2*2h+1-1 = 4*2h-1 < 4N

 

 

什么是区间加法

一个问题满足区间加法，仅当对于区间[L,R]的问题的答案可以由[L,M]和[M+1,R]的答案合并得到。经典的区间加法问题有：

满足区间加法的例子：

1，区间和        总区间和 = 左区间和+右区间和

2，最大公因数    总GCD  = GCD(左区间GCD，右区间GCD)

3，最大值        总最大值 = MAX(左区间MAX，右区间MAX)

不满足区间加法的例子：

1，区间众数           总区间总数无法根据左右区间总数求出来

2，最长递增序列长度    总区间最长递增长度无法直接由左右区间最长递增长度相加而得

线段树的原理及实现

注意：如果我没有特别申明的话，这里的询问全部都是区间求和

线段树主要是把一段大区间平均地划分成两段小区间进行维护，再用小区间的值来更新大区间。这样既能保证正确性，又能使时间保持在log级别（因为这棵线段树是平衡的）。也就是说，一个[L…R]的区间会被划分成[L…(L+R)/2]和[(L+R)/2+1…R]这两个小区间进行维护，直到L=R。

下图就是一棵[1, 5]的线段树的分解过程（相同颜色的节点在同一层）

 

 

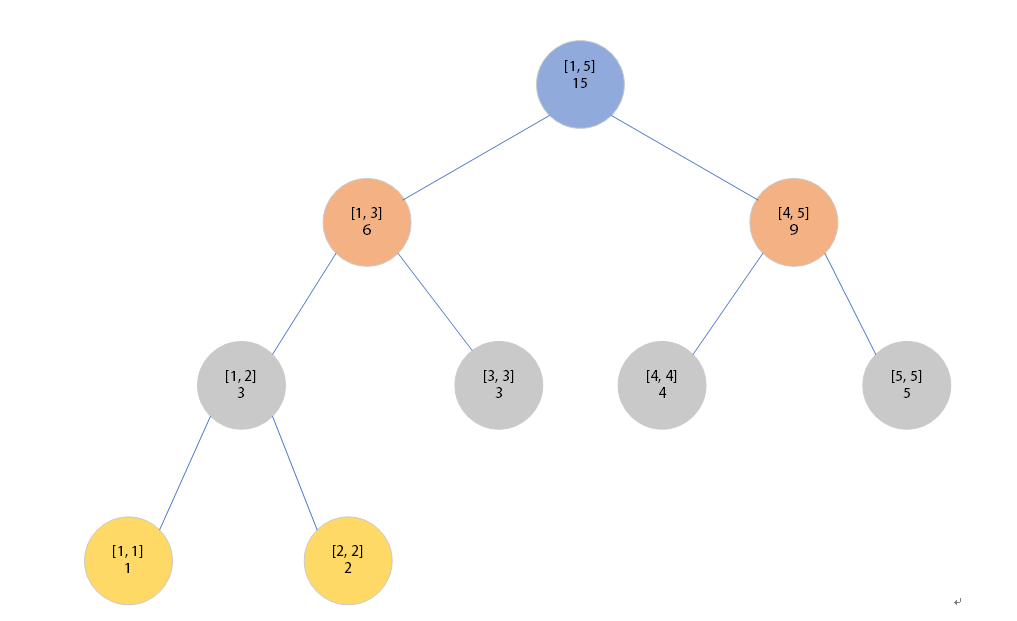
可以发现，这棵线段树的最大深度不超过[log2(n−1)]+2（其中[x]表示对x进行下取整）

a.储存方式

通常用的都是堆式储存法，即编号为n的节点的左儿子编号为n∗2，右儿子编号为n∗2+1，父节点编号为n/2用位运算优化一下，以上的节点编号就变成：

左儿子：n << 1 右儿子：n << 1|1 父节点：n >> 1

通常，每一个线段树上的节点储存的都是这几个变量：区间左边界，区间右边界，区间的答案（这里为区间元素之和）和懒惰标记

下面是线段树的定义：

const int maxh = 4*N;     
struct node      
{      int l;      //左边界     int r;      // 右边界     int val, lazy;    //节点所维护的区间[l, r]的权值, 懒惰标记      
}tree[maxh];//N为总节点数      
int val[maxh]; //原数组

b.初始化

常见的做法是遍历整棵线段树，给每一个节点赋值，注意要递归到线段树的叶节点才结束。

void pushup(int n)  
{  t[n].val = t[2*n].val+t[2*n+1].val;    //总区间和 = 左区间和+右区间和   
}  
void build(int n,int l,int r)  
{  t[n].l = l;     //记录维护的原数组的左端点   t[n].r = r;     //记录维护的右端点   t[n].lazy = 0;  //标记下懒惰数组   if(l==r){       //l==r,表示叶子节点,  t[n].val = val[l];    //因为l==r,那么这个节点维护的值就是原数组val[l]的值   return;  }         int mid = (l+r)>>1;  build(n*2,l,mid);      //递归建左子树   build(n*2+1,mid+1,r);  //递归建右子树  pushup(n);             //求该点的权值   
}

 

 

c.单点修改

时间复杂度：O(log2(N))

线段树的高度接近log2(N)：所以更新经过的节点数接近log2(N) 

当我们要把下标为idx的元素修改（加减乘除、赋值运算等），这里我们加上一个值C，可以递归向下找到叶结点，再向上更新，左节点维护的范围是[l, mid]，右节点维护的范围是[mid+1, r]。

如果：idx<=mid，那么val[idx]就由左节点维护，所有走左节点

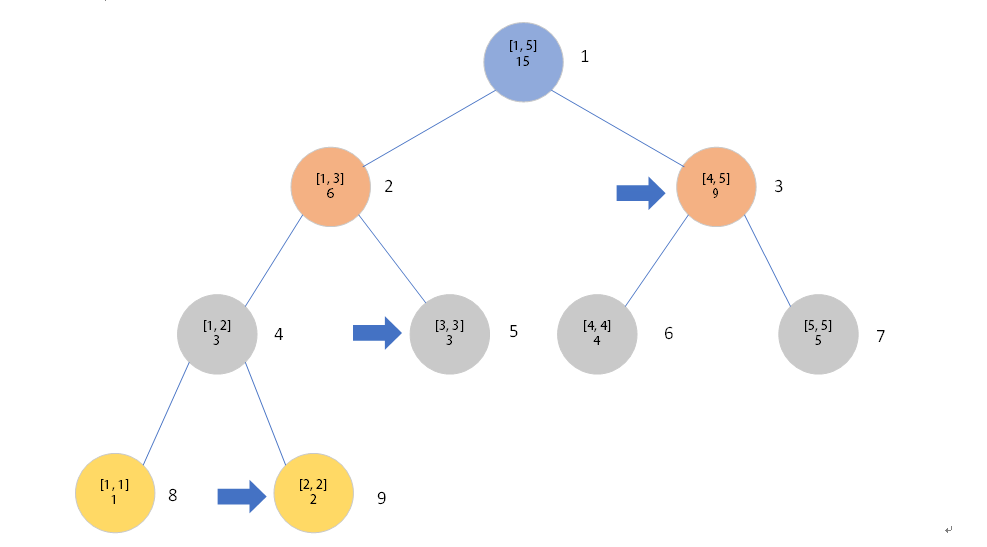
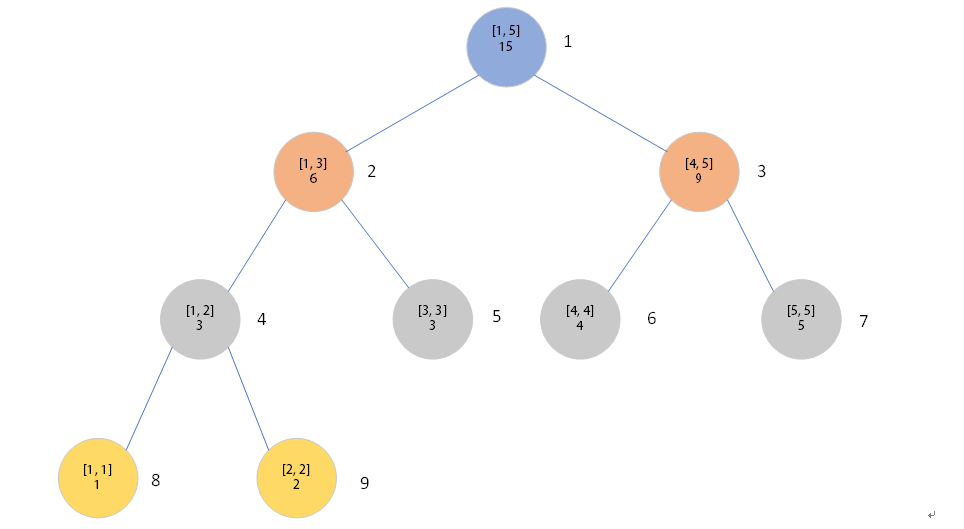
如果：mid

最后直到l==r的时候找到叶子节点，这个节点维护的范围就是[idx, idx]即val[idx]这个元素

修改这个叶子节点的权值，最后回溯向上修改沿途的节点权值

void updateOne(int n,int idx,int C)  
{  int l = t[n].l;//左端点   int r = t[n].r;//右端点   if(l==r)    //l==r,到了叶子节点   
    {  t[n].val += C;    //更新权值   return;   }     int mid = (l+r)>>1;  if(idx<=mid)     //val[idx]由左节点维护   updateOne(n*2,idx,C);  else          //val[idx]由右节点维护   updateOne(n*2+1,idx,C);  pushup(n);    //向上更新   
}

 

   

 

模拟更新[2, 5]，从n=1开始

第一轮：节点2：[1, 3]与待更新范围有交集要走，节点3：[4, 5]与待更新范围有交集要走

第二轮：节点4：[1, 2]有交集要走，节点5：[3, 3]有交集要走，节点[4, 5]被更新范围包括直接更新，lazy+=1不向下走。

第三轮：节点1：[1, 1]没有交集排除，节点9：[2, 2]被包括更新，节点3：[3, 3]被包括更新

结束!

 

时间复杂度：O(log2N)

定理：n>=3时，一个[1,n]的线段树可以将[1,n]的任意子区间[L,R]分解为不超过2|log2(N-1)| 向下取整子区间。

 

d.区间修改

待更新区间为[L, R]，左节点维护的区间[l, mid], 右节点维护的区间[mid+1, r]

L<=mid，左节点维护[l, mid]与[L, R]有交集要走

mid

如果[l, r]被[L, R]，直接更新，更新一下lazy标记，不往下走

递归进行直到更新结束

 

这里就要引入一样新的神奇的东西——懒惰标记！

懒惰标记

标记的含义：本区间已经被更新过了，但是子区间却没有被更新过，但是子结点暂时不更新，使用到时再更新，懒惰标记用于记录更新的信息（如果区间求和只用记录加了多少，而区间加减乘除等多种操作的问题则要记录进行的是哪一种操作，可能记录的信息会复杂一些）

这里再引入两个很重要的东西：相对标记和绝对标记。

相对标记&绝对标记

相对标记指的是可以共存的标记，且打标记的顺序与答案无关，即标记可以叠加。 比如说给一段区间中的所有数字都+a，我们就可以把标记叠加一下，比如上一次打了一个+1的标记，这一次要给这一段区间+2，那么就把+1的标记变成+3。

绝对标记是指不可以共存的标记，每一次都要先把标记下传，再给当前节点打上新的标记。这些标记不能改变次序，否则会出错。 比如说给一段区间的数字重新赋值，或是给一段区间进行多种操作。

有了懒惰标记这种神奇的东西，我们区间修改时就可以偷一下懒，先修改当前节点，然后直接把修改信息挂在节点上就可以了！

如下面这棵线段树，当我们要修改区间[1…4]，将元素赋值为1时，我们可以先找到所有的整个区间都要被修改的节点，显然是储存区间[1…3]和[4…4]的这两个节点。我们就可以先把[1…3]的sum改为3（(3−1+1)∗1=3,把[4…4]的sum改1（(1−1+1)∗1=1 然后给它们打上值为1的懒惰标记，然后就可以了。

比如下面这颗线段树，当我们修改[1, 4]区间都+1时我们先找到要修改的节点，就是t[2]和t[6]，之后修改权值，打上标记

t[2]={                                             t[6] = {

      l = 1;                                                          l = 4;   

      r = 3;                                                         r = 4;  

      val = 9;                                                      val = 5;

      lazy = 1;                                                    lazy = 1;   

}                                                           }    

 

 

 

这样一来，我们每一次修改区间时只要找到目标区间就可以了，不用再向下递归到叶节点。

下面是区间[L, R]+C的代码

void pushdown(int n)  
{  int l = t[n].l;  int r = t[n].r;  if(l==r)//叶子节点没有子结点   return;  if(t[n].lazy)//懒惰标记不为0才能向下更新   
    {     int mid = (l+r)/2;  t[2*n].val += t[n].lazy*(mid-l+1);//更新左节点权值   t[2*n+1].val += t[n].lazy*(r-mid);//更新右节点权值  t[2*n].lazy += t[n].lazy;         //更新左节点标记   t[2*n+1].lazy += t[n].lazy;       //更新右节点标记   t[n].lazy = 0;                    //清除标记      
    }  
}  
void updateRange(int n,int L,int R,int C)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //待更新区间为[L, R],而[l, r]是[L, R]的子集所以更新   
    {  t[n].val += (r-l+1)*C;    //更新权值   t[n].lazy += C;           //更新标记      return;  }  pushdown(n);    //向下更新   int mid = (l+r)>>1;  if(L<=mid)      //左节点维护的区间与[L, R]有交集   updateRange(2*n,L,R,C);  if(R>mid)      //右节点维护的区间与[L, R]有交集   updateRange(2*n+1,L,R,C);  pushup(n);     //向上更新   
}

 

e.区间查询

和区间修改一样的道理，这里是直接返回结果，区间修改是修改权值

int query(int n,int L,int R)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //被包括直接返回   return t[n].val;  pushdown(n);        //向下更新   int ans = 0;        //保持答案   int mid = (l+r)>>1;  if(L<=mid)           //查询区间与左节点维护区间有交集   ans += query(2*n,L,R);//加上左节点交集区间的答案   if(R>mid)  ans += query(2*n+1,L,R);//加上右节点交集区间的答案   return ans;  
}

 

模板：

#include   
using namespace std;  
const int N = 1e5+10;  
const int maxh = 4*N;     
struct node      
{      int l;      //左边界     int r;      // 右边界     int val, lazy;    //节点所维护的区间[l, r]的权值, 懒惰标记      
}t[maxh];//N为总节点数      
int val[maxh]; //原数组   void pushup(int n)  
{  t[n].val = t[2*n].val+t[2*n+1].val;    //总区间和 = 左区间和+右区间和   
}  
void build(int n,int l,int r)  
{  t[n].l = l;     //记录维护的原数组的左端点   t[n].r = r;     //记录维护的右端点   t[n].lazy = 0;  //标记下懒惰数组   if(l==r){       //l==r,表示叶子节点,  t[n].val = val[l];    //因为l==r,那么这个节点维护的值就是原数组val[l]的值   return;  }         int mid = (l+r)>>1;  build(n*2,l,mid);      //递归建左子树   build(n*2+1,mid+1,r);  //递归建左子树  pushup(n);             //求该点的权值   
}  
void updateOne(int n,int idx,int C)  
{  int l = t[n].l;//左端点   int r = t[n].r;//右端点   if(l==r)    //l==r,到了叶子节点   
    {  t[n].val += C;    //更新权值   return;   }     int mid = (l+r)>>1;  if(idx<=mid)     //val[idx]由左节点维护   updateOne(n*2,idx,C);  else          //val[idx]由右节点维护   updateOne(n*2+1,idx,C);  pushup(n);    //向上更新   
}   
void pushdown(int n)  
{  int l = t[n].l;  int r = t[n].r;  if(l==r)//叶子节点没有子结点   return;  if(t[n].lazy)//懒惰标记不为0才能向下更新   
    {     int mid = (l+r)/2;  t[2*n].val += t[n].lazy*(mid-l+1);//更新左节点权值   t[2*n+1].val += t[n].lazy*(r-mid);//更新右节点权值  t[2*n].lazy += t[n].lazy;         //更新左节点标记   t[2*n+1].lazy += t[n].lazy;       //更新右节点标记   t[n].lazy = 0;                    //清除标记      
    }  
}  
int query(int n,int L,int R)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //被包括直接返回   return t[n].val;  pushdown(n);        //向下更新   int ans = 0;        //保持答案   int mid = (l+r)>>1;  if(L<=mid)           //查询区间与左节点维护区间有交集   ans += query(2*n,L,R);//加上左节点交集区间的答案   if(R>mid)  ans += query(2*n+1,L,R);//加上右节点交集区间的答案   return ans;  
}  
void updateRange(int n,int L,int R,int C)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //待更新区间为[L, R],而[l, r]是[L, R]的子集所以更新   
    {  t[n].val += (r-l+1)*C;    //更新权值   t[n].lazy += C;           //更新标记      return;  }  pushdown(n);    //向下更新   int mid = (l+r)>>1;  if(L<=mid)      //左节点维护的区间与[L, R]有交集   updateRange(2*n,L,R,C);  if(R>mid)      //右节点维护的区间与[L, R]有交集   updateRange(2*n+1,L,R,C);  pushup(n);     //向上更新   
}  
int main()  
{  return 0;   
}

 

 

 

例题

HDU1166

https://vjudge.net/problem/HDU-1166

单点更新+区间查询

 

Input

第一行一个整数T，表示有T组数据。

每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。

接下来每行有一条命令，命令有4种形式：

(1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30）

(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）;

(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数;

(4)End 表示结束，这条命令在每组数据最后出现;

每组数据最多有40000条命令

Output

对第i组数据,首先输出“Case i:”和回车,

对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。

#include 
using namespace std;
const int N = 5e5+10;
const int maxh = 4*N;   
struct node    
{    int l;      //左边界   int r;      // 右边界   int val;    //节点所维护的区间[l, r]的权值 
}t[maxh];//N为总节点数    
int val[maxh]; //原数组 void pushup(int n)
{t[n].val = t[2*n].val+t[2*n+1].val;    //总区间和 = 左区间和+右区间和 
}
void build(int n,int l,int r)
{t[n].l = l;     //记录维护的原数组的左端点 t[n].r = r;     //记录维护的右端点 if(l==r){       //l==r,表示叶子节点,t[n].val = val[l];    //因为l==r,那么这个节点维护的值就是原数组val[l]的值 return;}       int mid = (l+r)>>1;build(n*2,l,mid);      //递归建左子树 build(n*2+1,mid+1,r);  //递归建左子树pushup(n);             //求该点的权值 
}
void updateOne(int n,int idx,int C)
{int l = t[n].l;//左端点 int r = t[n].r;//右端点 if(l==r)    //l==r,到了叶子节点 
    {t[n].val += C;    //更新权值 return; }   int mid = (l+r)>>1;if(idx<=mid)     //val[idx]由左节点维护 updateOne(n*2,idx,C);else          //val[idx]由右节点维护 updateOne(n*2+1,idx,C);pushup(n);    //向上更新 
} 
int query(int n,int L,int R)
{int l = t[n].l;int r = t[n].r;if(L<=l && r<=R)    //被包括直接返回 return t[n].val;int ans = 0;        //保持答案 int mid = (l+r)>>1;if(L<=mid)          //查询区间与左节点维护区间有交集 ans += query(2*n,L,R);//加上左节点交集区间的答案 if(R>mid)ans += query(2*n+1,L,R);//加上右节点交集区间的答案 return ans;
}
int main()
{int T;scanf("%d", &T);for(int cnt = 1;cnt <= T;cnt ++){int N;char op[10];printf("Case %d:
", cnt);scanf("%d", &N);for(int i = 1;i <= N;i ++)scanf("%d", &val[i]);    //数组的权值 build(1,1,N);                //建树 while(scanf("%s", op))      {if(op[0]=='E')          //END结束     break;int i, j;scanf("%d%d", &i, &j);if(op[0]=='A')          //ADD,第i个营地+j人 updateOne(1,i,j);else if(op[0]=='S')     //ADD,第i个营地-j人updateOne(1,i,-j);elseprintf("%d
", query(1,i,j));//查询i--j营地一共有多少人 
        }}return 0; 
}

 

 

 

HDU1754

https://vjudge.net/problem/HDU-1754

Input

多组测试，EOF结束

第一行，有两个正整数 N 和 M ( 0
学生ID编号分别从1编到N。 

第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩。 

接下来有M行。每一行有一个字符 C (只取'Q'或'U') ，和两个正整数A，B。 

当C为'Q'的时候，表示这是一条询问操作，它询问ID从A到B(包括A,B)的学生当中，成绩最高的是多少。 

当C为'U'的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。 

 

Output

对于每一次询问操作，在一行里面输出最高成绩。

 

#include  
#include  
using namespace std;  
const int N = 2e5+10;  
const int maxh = 4*N;     
struct node      
{      int l;      //左边界     int r;      // 右边界     int val;    //节点所维护的区间[l, r]的权值    
}t[maxh];//N为总节点数      
int val[maxh]; //原数组   void pushup(int n)  
{  t[n].val = max(t[2*n].val, t[2*n+1].val);    //总区间和 = 左区间和+右区间和   
}  
void build(int n,int l,int r)  
{  t[n].l = l;     //记录维护的原数组的左端点   t[n].r = r;     //记录维护的右端点   if(l==r){       //l==r,表示叶子节点,  t[n].val = val[l];    //因为l==r,那么这个节点维护的值就是原数组val[l]的值   return;  }         int mid = (l+r)>>1;  build(n*2,l,mid);      //递归建左子树   build(n*2+1,mid+1,r);  //递归建左子树  pushup(n);             //求该点的权值   
}  
void updateOne(int n,int idx,int C)  
{  int l = t[n].l;//左端点   int r = t[n].r;//右端点   if(l==r)    //l==r,到了叶子节点   
    {  t[n].val = C;    //更新权值   return;   }     int mid = (l+r)>>1;  if(idx<=mid)     //val[idx]由左节点维护   updateOne(n*2,idx,C);  else          //val[idx]由右节点维护   updateOne(n*2+1,idx,C);  pushup(n);    //向上更新   
}   int query(int n,int L,int R)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //被包括直接返回   return t[n].val;  int ans = 0;        //保持答案   int mid = (l+r)>>1;  if(L<=mid)           //查询区间与左节点维护区间有交集   ans = max(ans, query(2*n,L,R));//加上左节点交集区间的答案   if(R>mid)  ans = max(ans, query(2*n+1,L,R));//加上右节点交集区间的答案   return ans;  
}  int main()  
{  int N, M;while(scanf("%d%d", &N, &M)!=EOF){for(int i = 1;i <= N;i ++)scanf("%d", &val[i]);build(1,1,N);while(M--){char C; int A, B;getchar();scanf("%c%d%d", &C, &A, &B);if(C=='Q')printf("%d
", query(1,A,B));elseupdateOne(1,A,B);}}return 0;   
}

 

 

 

HDU1698

https://vjudge.net/problem/HDU-1698

Input

题目有多组输入：

第一行输入一个整数T，表示数据组数

对于每组输入：

第一行整数N：绳子有多少段，而默认每段绳子价值为1

第二行整数Q：表示更新操作的次数

接下来Q行每行输入：X Y Z：表示将[X, Y]段变为价值Z

 

Output

输出绳子的总价值

#include   
using namespace std;  
const int N = 1e5+10;  
const int maxh = 4*N;     
struct node      
{      int l;      //左边界     int r;      // 右边界     int val, lazy;    //节点所维护的区间[l, r]的权值, 懒惰标记      
}t[maxh];//N为总节点数      void pushup(int n)  
{  t[n].val = t[2*n].val+t[2*n+1].val;    //总区间和 = 左区间和+右区间和   
}  
void build(int n,int l,int r)  
{  t[n].l = l;     //记录维护的原数组的左端点   t[n].r = r;     //记录维护的右端点   t[n].lazy = 0;  //标记下懒惰数组   if(l==r){       //l==r,表示叶子节点,  t[n].val = 1;    //因为l==r,那么这个节点维护的值就是原数组val[l]的值   return;  }         int mid = (l+r)>>1;  build(n*2,l,mid);      //递归建左子树   build(n*2+1,mid+1,r);  //递归建左子树  pushup(n);             //求该点的权值   
}  
void pushdown(int n)  
{  int l = t[n].l;  int r = t[n].r;  if(l==r)//叶子节点没有子结点   return;  if(t[n].lazy)//懒惰标记不为0才能向下更新   
    {     int mid = (l+r)/2;  t[2*n].val = t[n].lazy*(mid-l+1);//更新左节点权值   t[2*n+1].val = t[n].lazy*(r-mid);//更新右节点权值  t[2*n].lazy = t[n].lazy;         //更新左节点标记   t[2*n+1].lazy = t[n].lazy;       //更新右节点标记   t[n].lazy = 0;                    //清除标记      
    }  
}  
void updateRange(int n,int L,int R,int C)  
{  int l = t[n].l;  int r = t[n].r;  if(L<=l && r<=R)    //待更新区间为[L, R],而[l, r]是[L, R]的子集所以更新   
    {  t[n].val = (r-l+1)*C;    //更新权值   t[n].lazy = C;           //更新标记      return;  }  pushdown(n);    //向下更新   int mid = (l+r)>>1;  if(L<=mid)      //左节点维护的区间与[L, R]有交集   updateRange(2*n,L,R,C);  if(R>mid)      //右节点维护的区间与[L, R]有交集   updateRange(2*n+1,L,R,C);  pushup(n);     //向上更新   
}  
int main()  
{  int T, cnt = 1;scanf("%d", &T);while(T--){int N, Q;scanf("%d", &N);build(1,1,N);scanf("%d", &Q);while(Q--){int X, Y, Z;scanf("%d%d%d", &X, &Y, &Z);updateRange(1,X,Y,Z);}printf("Case %d: The total value of the hook is %d.
", cnt++, t[1].val);   }return 0;   
}

 

 

 

转载于:https://www.cnblogs.com/YukiNote/p/11301577.html

更多相关：

  • java 读取excel_Java12POI操作Excel

            Apache POI是一个开源的利用Java读写Excel，WORD等微软OLE2组件文档的项目。        我的需求是对Excel的数据进行导入或将数据以Excel的形式导出。先上简单的测试代码：package com.xing.studyTest.poi;import java.io.FileInputSt...

  • C++ 生成随机数

    要取得[a,b)的随机整数，使用(rand() % (b-a))+ a; 要取得[a,b]的随机整数，使用(rand() % (b-a+1))+ a; 要取得(a,b]的随机整数，使用(rand() % (b-a))+ a + 1; 通用公式:a + rand() % n；其中的a是起始值，n是整数的范围。 要取得a到b之间的...

  • 基于C++的本征图像分解(Intrinsic Image Decomposition)

    利用本征图像分解(Intrinsic Image Decomposition)算法，将图像分解为shading(illumination) image 和 reflectance(albedo) image，计算图像的reflectance image。 Reflectance Image 是指在变化的光照条件下能够维持不变的图像部分...

  • 剑指offer：面试题39. 数组中出现次数超过一半的数字

    题目：面试题39. 数组中出现次数超过一半的数字 数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。 你可以假设数组是非空的，并且给定的数组总是存在多数元素。 示例 1: 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2 限制： 1 <= 数组长度 <= 50000 解题： cl...

  • 剑指offer：面试题33. 二叉搜索树的后序遍历序列

    题目：二叉搜索树的后序遍历序列 输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。 参考以下这颗二叉搜索树：      5     /    2   6   /  1   3示例 1： 输入: [1,6,3,2,5] 输出...

  • 边缘计算架构_Openshift为边缘计算提供三节点架构部署

    当一个IT组织开始走到需要实施网络边缘的旅程时，他们很快意识到面对的挑战与他们在传统数据中心内所经历的挑战不同。 第一个挑战是空间。与更大的核心或区域数据中心同类产品相比，许多边缘站点的物理尺寸更小，因此，需要仔细计划好，尝试在未为其专门设计的空间中安装硬件。  第二个挑战是运行环境。还必须解决的可能面对的冷热温度变化 ，天气，无...

  • node 获取表单数据 为空_数据结构与算法(python)单向循环链表

    单向循环链表单链表的一个变形是单向循环链表, 链表的最后一个节点的next域不再为None, 而是指向链表的头节点.单向循环链表如图所示:单向循环链表同样单向循环链表也是要使用python来对它的基本功能进行一个封装. 总体大致的功能如下:is_empty() 判断链表是否为空length() 返回链表的长度travel() 遍历ad...

  • 剑指offer：面试题36. 二叉搜索树与双向链表

    题目： 二叉搜索树与双向链表 输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。 为了让您更好地理解问题，以下面的二叉搜索树为例： 我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一...

  • 剑指offer：面试题18. 删除链表的节点

    题目：删除链表的节点 给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。 返回删除后的链表的头节点。 注意：此题对比原题有改动 示例 1: 输入: head = [4,5,1,9], val = 5 输出: [4,1,9] 解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为...

  • 从零开始的ROS四轴机械臂控制-目录

    【从零开始的ROS四轴机械臂控制】（一）- 实际模型制作、Solidworks文件转urdf与rviz仿真 一、模型制作 1.实际模型制作 2.Solidworks模型制作 二、Solidworks文件转urdf 1.sw_urdf_exporter插件 2.添加坐标系和转轴 3.导出urdf文件 三、rivz仿真...

©2024 11GX.COM